Důležitou částí termodynamiky je studium přeměn mezi různými fázemi látky, protože tyto procesy probíhají v praxi a mají zásadní význam pro předpovídání chování systému za určitých podmínek. Tyto transformace se nazývají fázové přechody, kterým je věnován článek.
Koncept fáze a součásti systému

Než přistoupíme k úvahám o fázových přechodech ve fyzice, je nutné definovat pojem fáze jako taková. Jak je známo z kurzu obecné fyziky, existují tři skupenství hmoty: plynné, pevné a kapalné. Ve zvláštní části vědy - v termodynamice - jsou zákony formulovány pro fáze hmoty, a ne pro jejich stavy agregace. Fáze je chápána jako určitý objem hmoty, který má homogenní strukturu, vyznačuje se specifickými fyzikálními a chemickými vlastnostmi a je oddělen od zbytku hmoty hranicemi, které se nazývají interfáze.
Pojem „fáze“tedy nese mnohem více prakticky významnějších informací o vlastnostechnež jeho stav agregace. Například pevné skupenství kovu, jako je železo, může být v následujících fázích: nízkoteplotní magnetický krychlový centrovaný na tělo (BCC), nízkoteplotní nemagnetický bcc, kubický centrovaný obličejem (fcc) a vysokoteplotní teplota nemagnetická bcc.
Kromě pojmu „fáze“používají zákony termodynamiky také termín „složky“, což znamená počet chemických prvků, které tvoří určitý systém. To znamená, že fáze může být buď jednosložková (1 chemický prvek) nebo vícesložková (několik chemických prvků).
Gibbsův teorém a rovnováha mezi fázemi systému

Pro pochopení fázových přechodů je nutné znát podmínky rovnováhy mezi nimi. Tyto podmínky lze matematicky získat řešením systému Gibbsových rovnic pro každou z nich za předpokladu, že rovnovážného stavu je dosaženo, když se celková Gibbsova energie systému izolovaného od vnějšího vlivu přestane měnit.
Výsledkem řešení naznačeného systému rovnic jsou získány podmínky pro existenci rovnováhy mezi několika fázemi: izolovaný systém se přestane vyvíjet pouze tehdy, když tlaky, chemické potenciály každé složky a teploty ve všech fázích jsou si navzájem rovny.
Gibbsovo fázové pravidlo pro rovnováhu

Systém skládající se z několika fází a komponent může být nejen v rovnovázeza určitých podmínek, například při určité teplotě a tlaku. Některé z proměnných v Gibbsově teorému pro rovnováhu lze měnit při zachování jak počtu fází, tak počtu složek, které jsou v této rovnováze. Počet proměnných, které lze změnit, aniž by došlo k narušení rovnováhy v systému, se nazývá počet svobod tohoto systému.
Počet volností l systému sestávajícího z f fází a k komponent je jednoznačně určen z Gibbsova fázového pravidla. Toto pravidlo je matematicky zapsáno následovně: l + f=k + 2. Jak s tímto pravidlem pracovat? Velmi jednoduché. Například je známo, že systém se skládá z f=3 rovnovážných fází. Jaký minimální počet komponent může takový systém obsahovat? Na otázku můžete odpovědět úvahou takto: v případě rovnováhy existují nejpřísnější podmínky, když je realizována pouze u určitých indikátorů, to znamená, že změna jakéhokoli termodynamického parametru povede k nerovnováze. To znamená, že počet svobod l=0. Dosazením známých hodnot l a f získáme k=1, to znamená, že systém, ve kterém jsou tři fáze v rovnováze, se může skládat z jedné složky. Ukázkovým příkladem je trojný bod vody, kde led, kapalná voda a pára existují v rovnováze při určitých teplotách a tlacích.
Klasifikace fázových transformací
Pokud začnete měnit některé termodynamické parametry v systému v rovnováze, můžete pozorovat, jak jedna fáze zmizí a další se objeví. Jednoduchým příkladem tohoto procesu je tání ledu při jeho zahřívání.
Vzhledem k tomu, že Gibbsova rovnice závisí pouze na dvou proměnných (tlaku a teplotě) a fázový přechod zahrnuje změnu těchto proměnných, pak lze matematicky přechod mezi fázemi popsat diferencováním Gibbsovy energie s ohledem na její proměnné. Právě tento přístup použil rakouský fyzik Paul Ehrenfest v roce 1933, když sestavil klasifikaci všech známých termodynamických procesů, ke kterým dochází při změně fázové rovnováhy.
Ze základů termodynamiky vyplývá, že první derivace Gibbsovy energie vzhledem k teplotě se rovná změně entropie systému. Derivace Gibbsovy energie vzhledem k tlaku se rovná změně objemu. Pokud se při změně fází v systému entropie nebo objem zlomí, to znamená, že se náhle změní, mluví se o fázovém přechodu prvního řádu.
Druhými derivacemi Gibbsovy energie s ohledem na teplotu a tlak jsou tepelná kapacita a koeficient objemové roztažnosti. Pokud je transformace mezi fázemi doprovázena nespojitostí hodnot uvedených fyzikálních veličin, pak se hovoří o fázovém přechodu druhého řádu.
Příklady transformací mezi fázemi

V přírodě existuje obrovské množství různých přechodů. V rámci této klasifikace jsou nápadnými příklady přechodů prvního druhu procesy tavení kovů nebo kondenzace vodní páry ze vzduchu, kdy dochází k objemovému skoku v systému.
Pokud mluvíme o přechodech druhého řádu, pak nápadnými příklady jsou transformace železa z magnetického do paramagnetického stavu při teplotě768 ºC nebo přeměna kovového vodiče do supravodivého stavu při teplotách blízkých absolutní nule.
Rovnice popisující přechody prvního druhu
V praxi je často nutné vědět, jak se v systému mění teplota, tlak a absorbovaná (uvolňovaná) energie, když v něm dochází k fázovým přeměnám. K tomuto účelu se používají dvě důležité rovnice. Získávají se na základě znalosti základů termodynamiky:
- Clapeyronův vzorec, který stanovuje vztah mezi tlakem a teplotou během transformací mezi různými fázemi.
- Clausiův vzorec, který spojuje absorbovanou (uvolněnou) energii a teplotu systému během transformace.
Využití obou rovnic je nejen při získávání kvantitativních závislostí fyzikálních veličin, ale také při určování znaménka sklonu rovnovážných křivek na fázových diagramech.
Rovnice pro popis přechodů druhého druhu

Fázové přechody 1. a 2. druhu jsou popsány různými rovnicemi, protože aplikace Clausiových a Clausiových rovnic pro přechody druhého řádu vede k matematické nejistotě.
K popisu posledně jmenovaného se používají Ehrenfestovy rovnice, které stanovují vztah mezi změnami tlaku a teploty na základě znalosti změn tepelné kapacity a koeficientu objemové roztažnosti během transformačního procesu. Ehrenfestovy rovnice se používají k popisu přechodů vodič-supravodič v nepřítomnosti magnetického pole.
Důležitéfázové diagramy
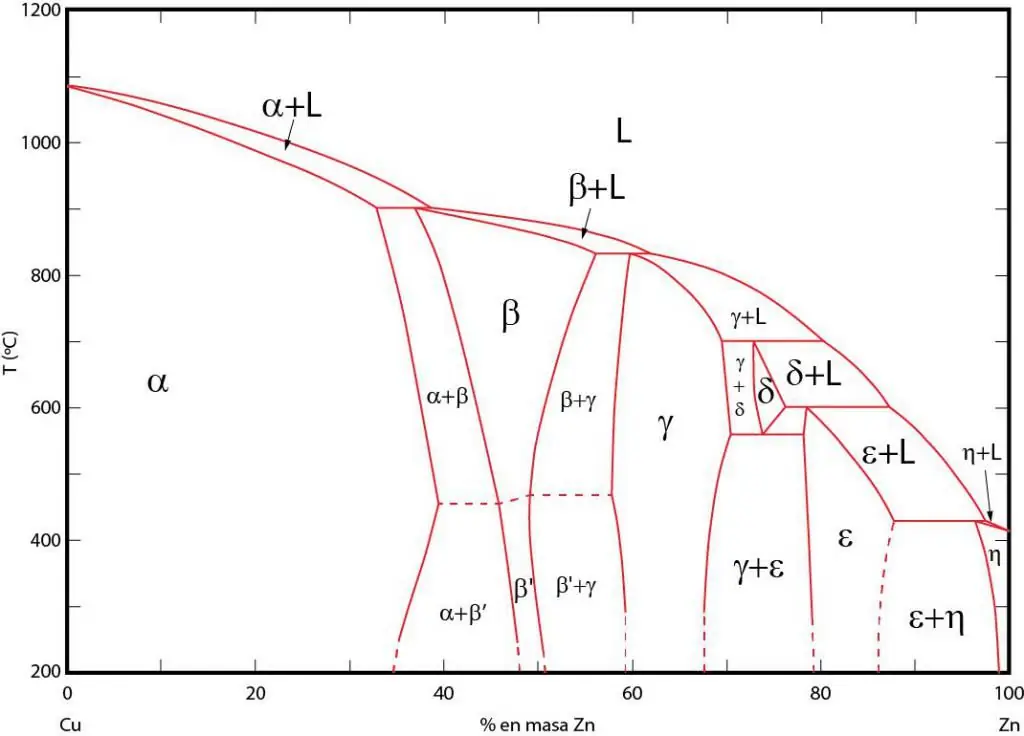
Fázové diagramy jsou grafickým znázorněním oblastí, ve kterých existují odpovídající fáze v rovnováze. Tyto oblasti jsou odděleny rovnovážnými liniemi mezi fázemi. Často se používají fázové diagramy P-T (tlak-teplota), T-V (teplota-objem) a P-V (tlak-objem).
Význam fázových diagramů spočívá v tom, že umožňují předvídat, v jaké fázi se systém bude nacházet, když se příslušně změní vnější podmínky. Tato informace se používá při tepelném zpracování různých materiálů za účelem získání struktury s požadovanými vlastnostmi.






