Lineární funkce je přímka nakreslená podél povrchu. Lze jej rozdělit na různé typy a modely. Níže budeme zvažovat vzorce pro jeho získání a také pro dosažení jeho dokonalosti v rovině. Na výkresech si to můžete plně ověřit a pochopit, jak by to mělo vypadat.
Lineární funkce y=kx + b
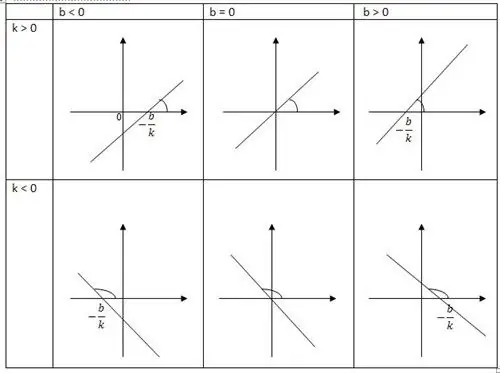
Tato hodnota je přesnou mírou proměnné v jednom pohledu. Inkrementace odkazuje na základní vlastnost lineární funkce, stává se úměrnou inkrementovanému argumentu. Jinými slovy, funkce představuje zobecnění přímé úměrnosti. Přímka je graf lineární funkce. Odtud pochází jeho název. Jedna reálná proměnná se dotýká jiné reálné funkce.
Vlastnosti
Lineární funkce je tvořící přímka přímky, která má kladný směr osy x. Jedním z jeho definujících součinitelů sklonu je k, určuje tečnu úhlu a. Přímka vytvořená v kladném směru osy x je k. Druhá souřadnice b označujesouřadnice bodu a také průsečík přímky s osou.
Co jsou to nelineární funkce?
Funkce, které nejsou lineární, se nazývají nelineární. Jedná se o matematický vztah mezi proměnnými. Nelineární nelze vyjádřit jako y=ax + b. Tento termín se používá v těch okamžicích, kdy je třeba studovat obecný případ. Tento proces začíná u nižších stupňů. V tomto případě jsou uvažovány kvadratické korekce. Taková funkce má spojité zakřivení.
Uvažovaná nelineární rovnice je libovolná. Příkladem nelineární funkce je y=x2. Často se používají termíny „lineární funkce“s upřesněním a přidáním výrazu „homogenní“. Může být aplikován na přesné lineární zobrazení X, což je vektorový prostor. Lineární funkce je celý systém jako on.






