Ze školy všichni známe pravidlo o umocňování: každé číslo s exponentem N se rovná výsledku vynásobení tohoto čísla N krát. Jinými slovy, 7 na mocninu 3 je samo sebou násobeno 7 třikrát, tedy 343. Dalším pravidlem je, že umocnění jakékoli hodnoty na 0 dává jedničku a zvýšení záporné hodnoty je výsledkem běžného umocňování, pokud je sudá, a stejný výsledek se znaménkem mínus, pokud je lichá.

Pravidla také dávají odpověď na to, jak zvýšit číslo na zápornou mocninu. K tomu je třeba obvyklým způsobem zvýšit požadovanou hodnotu modulem indikátoru a poté jednotku vydělit výsledkem.
Z těchto pravidel je zřejmé, že realizace skutečných úkolů s velkým množstvím bude vyžadovat dostupnost technických prostředků. Ručně bude možné násobit sám o sobě maximální rozsah čísel do dvaceti nebo třiceti, a pak ne více než třikrát nebo čtyřikrát. Nemluvě o tom, že pak také dělíme jednotku výsledkem. Proto pro ty, kteří nemají po ruce speciální strojírenstvíkalkulačce, ukážeme vám, jak zvýšit číslo na zápornou mocninu v Excelu.
Řešení problémů v Excelu
Pro řešení problémů s umocňováním vám Excel umožňuje použít jednu ze dvou možností.
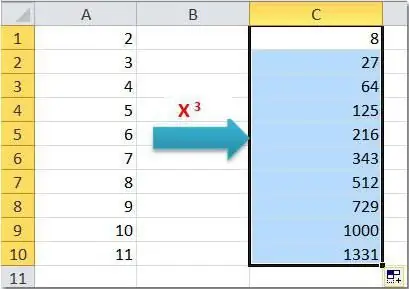
Prvním je použití vzorce se standardním symbolem čepice. Do buněk listu zadejte následující údaje:
| B | C | Formule | Výsledek | |
| 2 | 7 | 3 | =B2^C2 | 343 |
Stejným způsobem můžete zvýšit požadovanou hodnotu na libovolnou mocninu - zápornou, zlomkovou. Udělejme následující a odpovězme na otázku, jak zvýšit číslo na zápornou mocninu. Příklad:
| B | C | Formule | Výsledek | |
| 2 | 7 | -3 | =B2^C2 | 0, 002915 |
=B2^-C2 můžete opravit přímo ve vzorci.
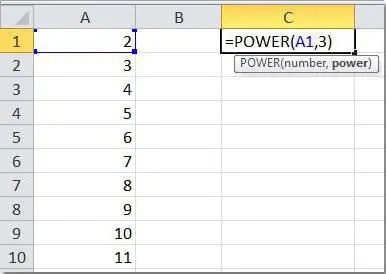
Druhou možností je použití hotové funkce „Stupeň“, která přebírá dva povinné argumenty - číslo a indikátor. Chcete-li jej začít používat, stačí do libovolné volné buňky vložit znak „rovná se“(=),ukazující na začátek vzorce a zadejte výše uvedená slova. Zbývá vybrat dvě buňky, které se zúčastní operace (nebo zadat konkrétní čísla ručně), a stisknout klávesu Enter. Podívejme se na několik jednoduchých příkladů.
| B | C | Formule | Výsledek | ||
| 2 | 7 | 3 | =POWER(B2;C2) | 343 | |
| 3 | 7 | -3 | =POWER(B3;C3) |
|
Jak vidíte, není nic složitého na tom, jak zvýšit číslo na zápornou mocninu a na normální mocninu pomocí Excelu. Koneckonců, k vyřešení tohoto problému můžete použít jak známý symbol „víka“, tak snadno zapamatovatelnou vestavěnou funkci programu. To je jednoznačné plus!
Přejděme ke složitějším příkladům. Připomeňme si pravidlo o tom, jak umocnit číslo na zápornou mocninu zlomkového znaku, a uvidíme, že tento úkol lze v Excelu vyřešit velmi snadno.
Zlomkové ukazatele
Stručně řečeno, algoritmus pro výpočet čísla se zlomkovým exponentem je následující.
- Převeďte zlomek na správný nebo nesprávný zlomek.
- Zvyšte naše číslo na čitatel výsledného převedeného zlomku.
- Z čísla získaného v předchozím odstavci vypočítejte odmocninu s podmínkou, že exponent odmocninybude jmenovatelem zlomku získaného v první fázi.
Souhlaste s tím, že i při práci s malými čísly a správnými zlomky mohou takové výpočty zabrat spoustu času. Je dobře, že tabulkovému procesoru Excel je jedno, jaké číslo a do jaké míry zvýšit. Zkuste vyřešit následující příklad na listu aplikace Excel:
| B (číslo) | C | Převést na zlomek | Formule | Výsledek | |
| 2 | 7 | 0, 4 | 2/5 | =POWER(B2;C2) | 2, 177906424 |
Pomocí výše uvedených pravidel můžete zkontrolovat a ujistit se, že výpočet je správný.
Na konci našeho článku ve formě tabulky se vzorci a výsledky uvedeme několik příkladů, jak umocnit číslo na zápornou mocninu, a také několik příkladů se zlomkovými čísly a mocninami.
Ukázková tabulka
Zkontrolujte následující příklady na listu Excel. Aby vše fungovalo správně, musíte při kopírování vzorce použít smíšený odkaz. Opravte číslo sloupce obsahujícího číslo, které se zvyšuje, a číslo řádku obsahujícího indikátor. Váš vzorec by měl vypadat nějak takto: "=$B4^C$3".
| Číslo / Stupeň | 1 | 2 | 3 | 0, 5 | -0, 5 |
| 1 | 1 | 1 | 1 | 1 | 1 |
| 2 | 2 | 4 | 8 | 1, 414214 | 0, 707107 |
| 7 | 7 | 49 | 343 | 2, 645751 | 0, 377964 |
| -7 | -7 | 49 | -343 |
NUMBER! |
NUMBER! |
| 0, 2 | 0, 2 | 0, 04 | 0, 008 | 0, 447214 | 2, 236068 |
| 0, 4 | 0, 4 | 0, 16 | 0, 064 | 0, 632456 | 1, 581139 |
| -0, 4 | -0, 4 | 0, 16 | -0, 064 | NUMBER! | NUMBER! |
Upozorňujeme, že kladná čísla (i neceločíselná) se bez problémů počítají pro jakékoli exponenty. Nejsou žádné problémy se zvyšováním jakýchkoli čísel na celá čísla. Ale zvýšení záporného čísla na zlomkovou mocninu se pro vás změní v chybu, protože není možné dodržet uvedené pravidlona začátku našeho článku o konstrukci záporných čísel, protože parita je charakteristikou výhradně INTEGER čísla.






