Ohmův zákon je základním zákonem elektrických obvodů. Zároveň nám umožňuje vysvětlit mnoho přírodních jevů. Lze například pochopit, proč elektřina „nebije“ptáky, kteří sedí na drátech. Pro fyziku je Ohmův zákon mimořádně významný. Bez jeho vědomí by nebylo možné vytvořit stabilní elektrické obvody nebo by neexistovala vůbec žádná elektronika.
Závislost I=I(U) a její hodnota
Historie objevu odolnosti materiálů přímo souvisí s charakteristikou proud-napětí. co to je Vezměme obvod s konstantním elektrickým proudem a uvažujme kterýkoli z jeho prvků: lampu, plynové potrubí, kovový vodič, baňku s elektrolytem atd.
Změnou napětí U (často označovaného jako V) přiváděného do příslušného prvku budeme sledovat změnu síly proudu (I), který jím prochází. V důsledku toho získáme závislost tvaru I \u003d I (U), která se nazývá „napěťová charakteristika prvku“a je přímým indikátorem jehoelektrické vlastnosti.
V/A charakteristika může pro různé prvky vypadat odlišně. Jeho nejjednodušší forma je získána uvažováním kovového vodiče, který vytvořil Georg Ohm (1789 - 1854).
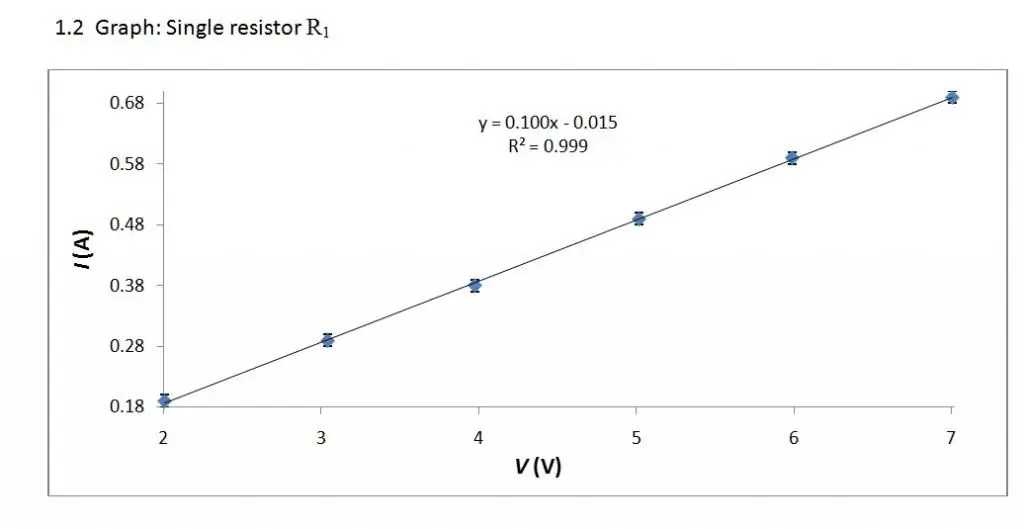
Voltampérová charakteristika je lineární vztah. Proto je jeho graf přímá.
Zákon ve své nejjednodušší podobě
Ohmův výzkum proudově-napěťových charakteristik vodičů ukázal, že síla proudu uvnitř kovového vodiče je úměrná rozdílu potenciálu na jeho koncích (I ~ U) a nepřímo úměrná určitému koeficientu, tj. I ~ 1/R. Tento koeficient se stal známým jako „odpor vodiče“a jednotka měření elektrického odporu byla Ohm nebo V/A.
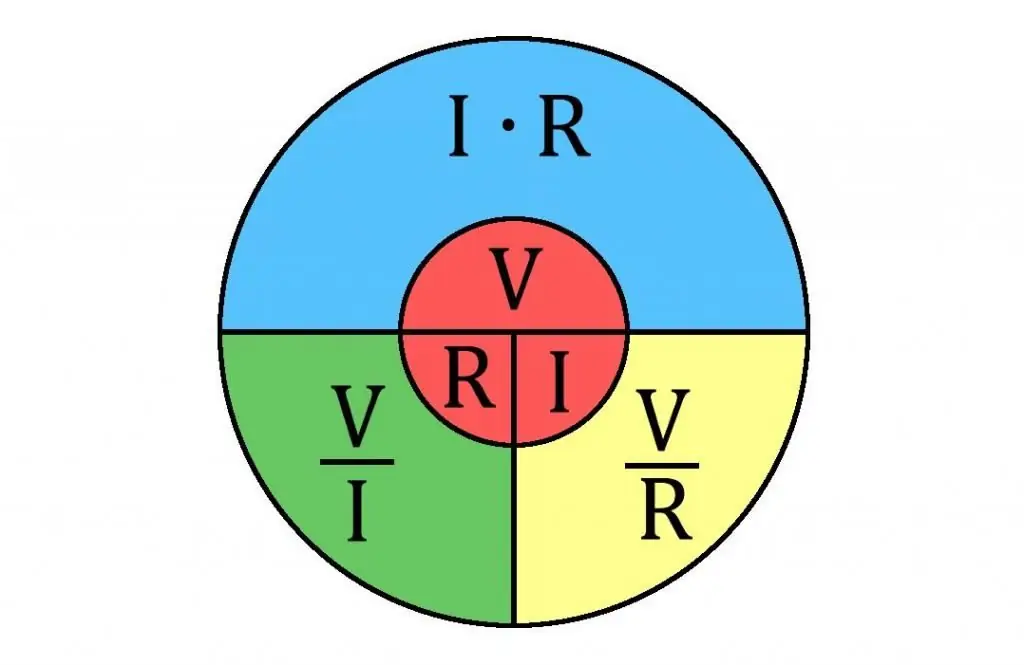
Ještě jedna věc, kterou je třeba poznamenat. Ohmův zákon se často používá k výpočtu odporu v obvodech.
Znění zákona
Ohmův zákon říká, že proudová síla (I) jedné části obvodu je úměrná napětí v této části a nepřímo úměrná jejímu odporu.
Je třeba poznamenat, že v této podobě platí zákon pouze pro homogenní část řetězce. Homogenní je ta část elektrického obvodu, která neobsahuje zdroj proudu. Jak používat Ohmův zákon v nehomogenním obvodu bude diskutováno níže.
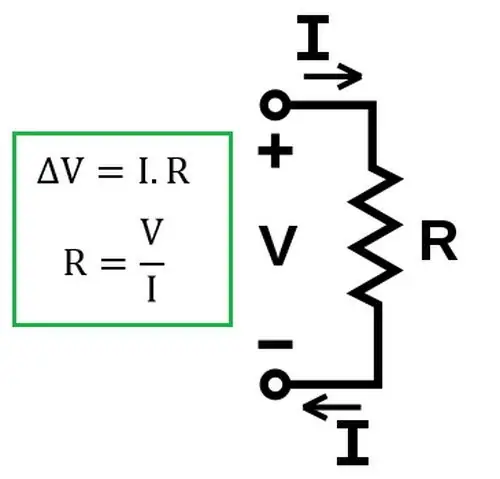
Později bylo experimentálně zjištěno, že zákon zůstává platný pro řešeníelektrolyty v elektrickém obvodu.
Fyzikální význam odporu
Odpor je vlastnost materiálů, látek nebo médií bránit průchodu elektrického proudu. Kvantitativně odpor 1 ohm znamená, že vodičem s napětím 1 V na jeho koncích může procházet elektrický proud 1 A.
Elektrický odpor
Experimentálně bylo zjištěno, že odpor elektrického proudu vodiče závisí na jeho rozměrech: délka, šířka, výška. A také na jeho tvaru (koule, válec) a materiálu, ze kterého je vyroben. Vzorec pro měrný odpor, například homogenního válcového vodiče, tedy bude: R \u003d pl / S.
Pokud do tohoto vzorce vložíme s=1 m2 a l=1 m, pak se R bude číselně rovnat p. Odtud se vypočítá měrná jednotka pro koeficient odporu vodiče v SI - to je Ohmm.

Ve vzorci měrného odporu je p koeficient odporu určený chemickými vlastnostmi materiálu, ze kterého je vodič vyroben.
Abychom zvážili diferenciální formu Ohmova zákona, musíme zvážit několik dalších konceptů.
Aktuální hustota
Jak víte, elektrický proud je přísně uspořádaný pohyb jakýchkoli nabitých částic. Například v kovech jsou proudovými nosiči elektrony a ve vodivých plynech ionty.
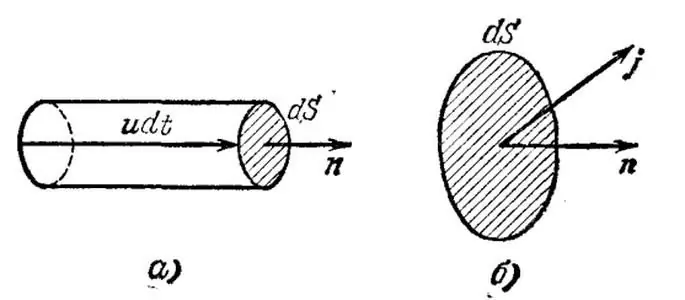
Vezměte si triviální případ, když všichni aktuální dopravcihomogenní - kovový vodič. V duchu vyčleníme nekonečně malý objem v tomto vodiči a označme u průměrnou (drift, uspořádanou) rychlost elektronů v daném objemu. Dále, nechť n označuje koncentraci aktuálních nosičů na jednotku objemu.
Nyní nakreslíme nekonečně malou plochu dS kolmou k vektoru u a sestrojíme podél rychlosti nekonečně malý válec s výškou udt, kde dt označuje dobu, za kterou projdou všechny aktuální nosiče rychlosti obsažené v uvažovaném objemu přes oblast dS.
V tomto případě bude náboj rovný q=neudSdt přenesen elektrony přes oblast, kde e je náboj elektronu. Hustota elektrického proudu je tedy vektor j=neu, označující množství náboje přeneseného za jednotku času přes jednotkovou plochu.
Jednou z výhod diferenciální definice Ohmova zákona je, že se často obejdete bez výpočtu odporu.
Elektrický náboj. Síla elektrického pole
Síla pole spolu s elektrickým nábojem je základním parametrem v teorii elektřiny. Zároveň o nich lze získat kvantitativní představu z jednoduchých experimentů dostupných školákům.
Pro jednoduchost budeme uvažovat elektrostatické pole. Jedná se o elektrické pole, které se s časem nemění. Takové pole může být vytvořeno stacionárními elektrickými náboji.
Pro naše účely je také potřeba zkušební nabití. V jeho kapacitě využijeme nabité těleso - tak malé, že není schopné způsobitjakékoli poruchy (přerozdělení nábojů) v okolních objektech.
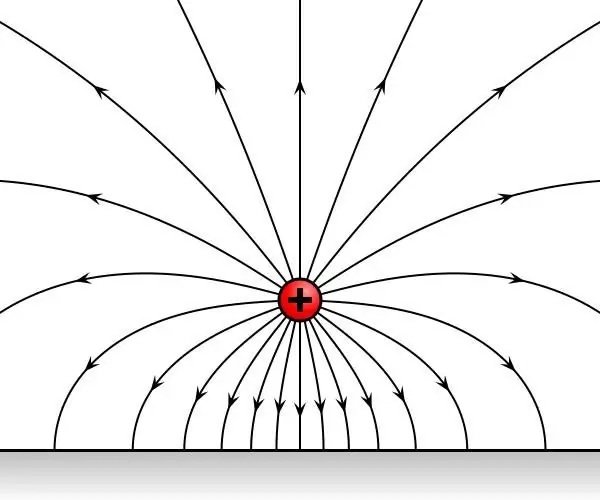
Uvažujme postupně dva odebrané testovací náboje, postupně umístěné v jednom bodě prostoru, který je pod vlivem elektrostatického pole. Ukazuje se, že obvinění budou z jeho strany vystavena časově neměnnému vlivu. Nechť F1 a F2 jsou síly působící na náboje.
Výsledkem zobecnění experimentálních dat bylo zjištěno, že síly F1 a F2 směřují buď v jedné, resp. v opačných směrech a jejich poměr F1/F2 je nezávislý na bodě v prostoru, kde byly střídavě umístěny testovací náboje. Proto je poměr F1/F2 charakteristikou samotných nábojů a nezávisí na poli.
Odhalení této skutečnosti umožnilo charakterizovat elektrizaci těles a bylo později nazýváno elektrickým nábojem. Z definice tedy vyplývá q1/q2=F1/F 2 , kde q1 a q2 - částka poplatků umístěných v jednom bodě pole a F 1 a F2 - síly působící na náboje ze strany pole.
Na základě těchto úvah byly experimentálně stanoveny velikosti nábojů různých částic. Podmíněným nastavením jednoho ze zkušebních nabití na hodnotu jednoho v poměru můžete vypočítat hodnotu druhého nabití měřením poměru F1/F2.
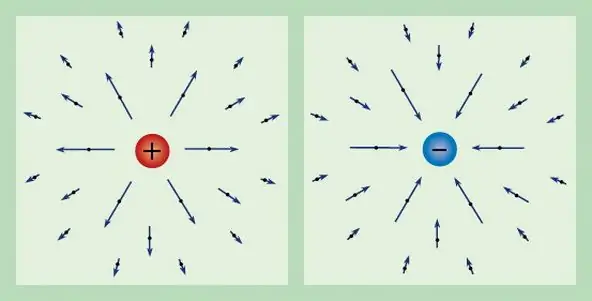
Jakékoli elektrické pole lze charakterizovat pomocí známého náboje. Síla působící na jednotkový zkušební náboj v klidu se tedy nazývá intenzita elektrického pole a značí se E. Z definice náboje získáme, že vektor síly má následující tvar: E=F/q.
Spojení vektorů j a E. Další forma Ohmova zákona
V homogenním vodiči bude uspořádaný pohyb nabitých částic probíhat ve směru vektoru E. To znamená, že vektory j a E budou spoluřízeny. Stejně jako při určování proudové hustoty volíme ve vodiči nekonečně malý válcový objem. Potom bude průřezem tohoto válce procházet proud rovný jdS a napětí aplikované na válec bude rovné Edl. Vzorec pro měrný odpor válce je také znám.
Poté, když vzorec pro proudovou sílu napíšeme dvěma způsoby, dostaneme: j=E/p, kde hodnota 1/p se nazývá elektrická vodivost a je inverzí k elektrickému odporu. Obvykle se označuje σ (sigma) nebo λ (lambda). Jednotkou vodivosti je Sm/m, kde Sm je Siemens. Jednotka inverzní k Ohm.
Takže můžeme odpovědět na výše položenou otázku o Ohmově zákonu pro nehomogenní obvod. V tomto případě budou nositele proudu ovlivňovány silou z elektrostatického pole, které je charakterizováno intenzitou E1, a dalšími silami, které na ně působí z jiného zdroje proudu, který může být označené E 2. Pak platil Ohmův zákonnehomogenní část řetězce bude vypadat takto: j=λ(E1 + E2).
Více o vodivosti a odporu
Schopnost vodiče vést elektrický proud je charakterizována jeho měrným odporem, který lze zjistit pomocí vzorce měrného odporu neboli vodivosti, vypočítané jako převrácená hodnota vodivosti. Hodnota těchto parametrů je dána jak chemickými vlastnostmi materiálu vodiče, tak vnějšími podmínkami. Zejména okolní teplota.
U většiny kovů je měrný odpor při normální teplotě úměrný tomu, tj. p ~ T. Při nízkých teplotách jsou však pozorovány odchylky. Pro velké množství kovů a slitin při teplotách blízkých 0°K ukázal výpočet odporu nulové hodnoty. Tento jev se nazývá supravodivost. Tuto vlastnost má například rtuť, cín, olovo, hliník atd. Každý kov má svou kritickou teplotu Tk, při které je pozorován jev supravodivosti.
Všimněte si také, že definici měrného odporu válce lze zobecnit na dráty vyrobené ze stejného materiálu. V tomto případě bude plocha průřezu ze vzorce měrného odporu rovna průřezu drátu a l - jeho délce.






