Jedním z hlavních úkolů analýzy dynamických řídicích systémů je řešení problému jejich stability. Jejich stabilita je jednou z nejdůležitějších charakteristik koncepce řízení. Systém je považován za nestabilní, pokud se nevrátí do své původní polohy, ale pokračuje v oscilaci poté, co prošel určitými změnami na vstupu, nebo je pod vlivem nechtěné poruchy.
Definice hlavního konceptu
Podle konceptu stability systému je stav jeho rovnováhy způsoben nepřítomností vlivu rušivých faktorů na něj. V této situaci má rozdíl mezi nastaveným a skutečným stavem tendenci k nule. Stabilita je její schopnost vrátit se do původního rovnovážného stavu poté, co skončí porucha, která vedla k jejímu narušení. Nestabilní systém se vlivem poruchy vzdaluje od rovnovážného stavu nebo osciluje, jehož amplituda postupněstoupá.

Podmínky stability
Pro stabilitu systému s konstantním časem musí být splněny následující dvě podmínky:
- Vytvoří omezený výstup pro každý vstup; pokud neexistuje žádný vstup, výstup musí být nula, bez ohledu na jakékoli počáteční podmínky.
- Stabilitu systému lze nazvat absolutní nebo relativní stabilitou. Prezentovaný termín se používá ve vztahu ke studii, ve které se porovnávají určité veličiny, jejich provozní podmínky. Stabilita je konečný výsledek vytvořený výsledkem.
Pokud je výstup systému nekonečný, i když je na něj aplikován konečný vstup, pak bude považován za nestabilní, tj. inherentně stabilní, má ohraničené zakončení, když je na něj aplikován omezený začátek sám.
Vstupem se v tomto případě rozumí různé body aplikace vlivu vnějšího prostředí na systém. Výstup je konečným produktem jeho činnosti, který má podobu transformovaných vstupních dat.
V kontinuálním lineárním časovém systému lze podmínku stability zapsat pro konkrétní impulsní odezvu.
Pokud je diskrétní, lze index stability zapsat také pro konkrétní impulsní odezvu.
Pro nestabilní podmínky ve spojitých i omezených systémech budou tyto výrazy nekonečné.
Typy stability a narušení
Ve statickém stavuStabilita systému je chápána jako jeho schopnost po malém narušení zajistit obnovení původního (nebo původního) režimu. Pod konceptem prezentovaným v této souvislosti uvažují kolísání, které ovlivňuje jeho chování, bez ohledu na to, kde se vlna nebo pokles objeví a jaká je jejich velikost. Na základě toho nám tyto režimy, které se blíží původnímu, umožňují považovat jej za lineární.
Dynamická stabilita systémů je schopnost systémů obnovit počáteční stav po velké poruše.
Velkým kolísáním se rozumí takový pohyb, jehož povaha vlivu a jeho odpovídající chování určuje dobu existence, velikost a místo jeho vzniku.
Na základě toho je systém v tomto rozsahu definován jako nelineární.
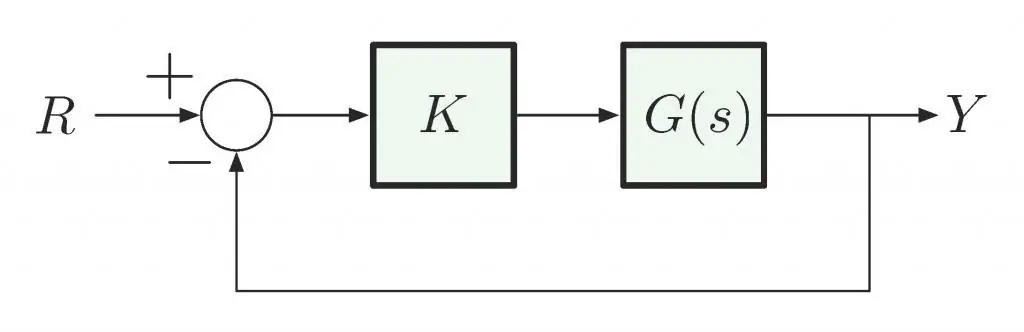
Kritéria pro stanovení udržitelnosti
Hlavní podmínkou stability lineárního systému není povaha poruchy, ale její struktura. Předpokládá se, že tato stabilita „v malém“je určena, pokud nejsou stanoveny její hranice. Stabilita "ve velkém" je určena limity a korespondencí skutečných odchylek s těmito stanovenými limity.
K určení stability systému se používají následující kritéria:
- kořenové kritérium;
- Stodolské kritérium;
- Hurwitzovo kritérium;
- Nyquistovo kritérium;
- Michajlovovo kritérium a další
K určení stability jednotlivých odkazů se používá kořenové kritérium a Stodolova vyhodnocovací technikaa otevřené systémy. Hurwitzovo kritérium je algebraické a umožňuje bez prodlení určit stabilitu uzavřených systémů. Nyquistova a Michajlovova kritéria jsou frekvenční. Používají se k určení stability uzavřených systémů na základě jejich frekvenční odezvy.

Kořenové kritérium
Umožňuje určit stabilitu systému na základě formy přenosové funkce. Jeho vlastnosti chování jsou popsány charakteristickým polynomem (jmenovatelem přenosové funkce). Pokud přiřadíme jmenovateli nule, kořeny výsledné rovnice nám umožní určit stupeň stability.
Podle tohoto kritéria bude lineární systém stabilní, pokud všechny kořeny rovnice budou v levé polorovině. Pokud se alespoň jeden z nich nachází na hranici stability, bude také na hranici. Pokud je alespoň jeden z nich v pravé polorovině, systém může být považován za nestabilní.
Stodola Criterion
Vyplývá to z kořenové definice. V souladu se Stodolovým kritériem lze lineární systém považovat za stabilní, pokud jsou všechny koeficienty polynomu kladné.
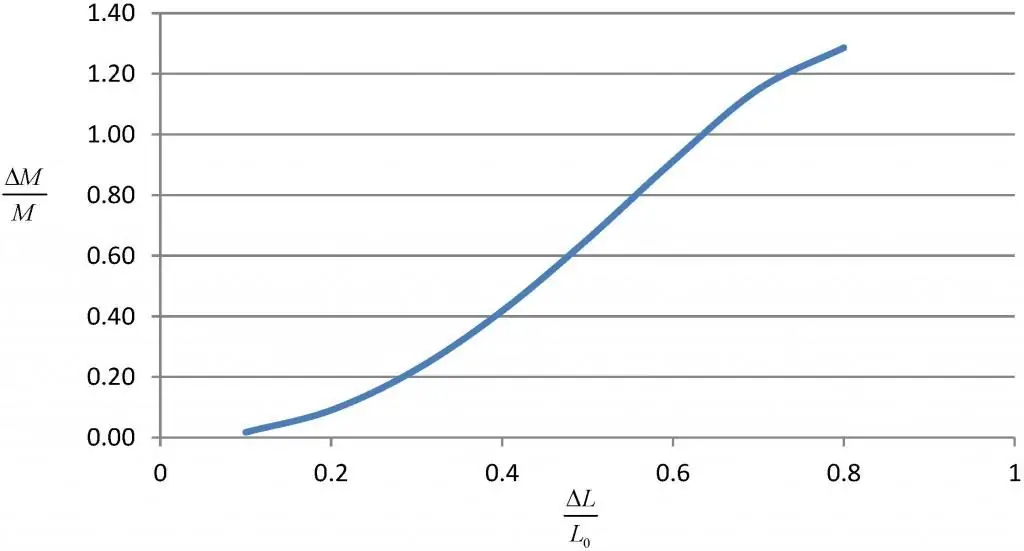
Hurwitzovo kritérium
Toto kritérium se používá pro charakteristický polynom uzavřeného systému. Podle této techniky je dostatečnou podmínkou stability skutečnost, že hodnota determinantu a všech hlavních diagonálních minorů matice je větší než nula. Pokud je alespoň jeden z nich stejnýnula, uvažuje se na hranici stability. Pokud existuje alespoň jeden negativní determinant, měl by být považován za nestabilní.
Nyquistovo kritérium
Základem této techniky je konstrukce křivky spojující konce vektoru proměnné, která zobrazuje přenosovou funkci. Formulace kritéria je následující: uzavřený systém je považován za stabilní, pokud funkční křivka neobklopuje bod se souřadnicemi (-1, j0) v komplexní rovině.
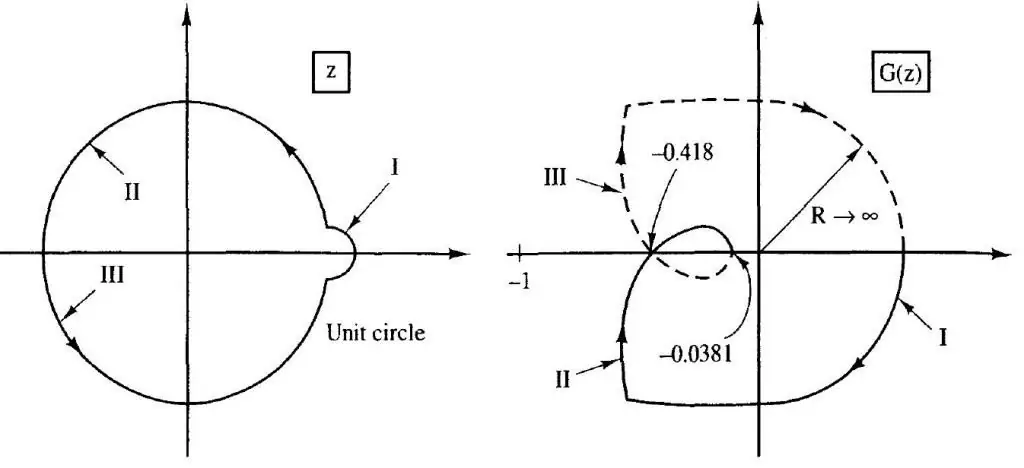
Systém finanční spolehlivosti
Finanční odolnost je stav, ve kterém je systém, tj. klíčové trhy a instituce, odolný vůči ekonomickým otřesům a připravený hladce plnit své základní funkce, jako je zprostředkování peněžních toků, řízení rizik a platební styk.
Vzhledem k vzájemné závislosti poskytování výkladu (vertikálně i horizontálně) musí analýza pokrývat celý systém finančního zprostředkování. Jinými slovy, kromě bankovního sektoru je třeba analyzovat i nebankovní instituce, které se v té či oné formě zabývají zprostředkováním. Patří mezi ně četné typy institucí, včetně makléřských firem, investičních fondů, pojišťoven a dalších (různých) subjektů. Při analýze systému finanční stability se zkoumá, do jaké míry je celá struktura schopna odolat vnějším a vnitřním šokům. Ke krizím samozřejmě nevedou vždy šoky, ale nestabilní finanční prostředí samotnésama o sobě může bránit zdravému rozvoji ekonomiky.
Příčiny finanční nestability identifikují různé teorie. Jejich význam se může lišit v závislosti na období a zemích zahrnutých do rozsahu analýzy. Mezi problematické faktory ovlivňující celý finanční systém literatura obvykle označuje následující:
- rychlá liberalizace finančního sektoru;
- nedostatečná hospodářská politika;
- Mechanismus necíleného směnného kurzu;
- neefektivní alokace zdrojů;
- slabý dohled;
- Neadekvátní regulace účetnictví a auditu.
Možné příčiny se objevují nejen hromadně, ale i jednotlivě nebo v náhodné kombinaci, proto je analýza finanční stability mimořádně obtížným úkolem. Zaměření na jednotlivá odvětví zkresluje celkový obraz, takže při studiu finanční stability je třeba tyto problémy posuzovat v jejich komplexnosti.

Proces analýzy stability podnikového systému probíhá v několika fázích.
Na začátku jsou vyhodnocovány a analyzovány absolutní a relativní ukazatele finanční stability. Ve druhé fázi jsou faktory rozděleny podle jejich významnosti, jejich vliv je kvalitativně a kvantitativně hodnocen.
Poměry finanční síly podniků
Finanční situace firmy, její stabilita do značné míry závisí na optimální struktuře kapitálových zdrojů, tedy poměru dluhu k vlastním zdrojům, na optimálnístruktuře majetku společnosti a především na poměru stálých a oběžných aktiv, jakož i stavu prostředků a pasiv společnosti.
Je proto důležité prostudovat strukturu zdrojů rizikového kapitálu a posoudit míru finanční stability a rizika. Pro tento účel se používají koeficienty stability systému:
- koeficient autonomie (nezávislosti) - podíl kapitálu v rozvaze;
- poměr závislosti - podíl vypůjčeného kapitálu v rozvaze;
- současná zadluženost - poměr krátkodobých finančních závazků k rozvaze;
- poměr finanční stability (dlouhodobá finanční nezávislost) - poměr kapitálu a dlouhodobého dluhu k rozvaze;
- poměr krytí dluhu (solvency ratio) - poměr kapitálu k dluhu;
- finanční pákový poměr (poměr finančního rizika) - poměr dluhu ke kapitálu.

Čím vyšší je úroveň ukazatelů, jako je autonomie, finanční stabilita, krytí dluhového kapitálu, tím nižší je úroveň další skupiny koeficientů (závislost, aktuální zadlužení, dlouhodobé závazky vůči investorům) a v souladu s tím i stabilita finanční situace společnosti. Finanční páka se také nazývá finanční páka.






