Studium vlastností ideálního plynu je důležité téma ve fyzice. Úvod do charakteristik plynových soustav začíná úvahou o Boyle-Mariotteově rovnici, protože jde o první experimentálně objevený zákon ideálního plynu. Podívejme se na to podrobněji v článku.
Co znamená ideální plyn?
Než budeme mluvit o Boyleově-Mariotteově zákoně a rovnici, která jej popisuje, pojďme definovat ideální plyn. Běžně se chápe jako tekutá látka, ve které částice, které ji tvoří, spolu neinteragují a jejich velikosti jsou zanedbatelně malé ve srovnání s průměrnými vzdálenostmi mezi částicemi.
Ve skutečnosti je každý plyn skutečný, to znamená, že jeho jednotlivé atomy a molekuly mají určitou velikost a neinteragují spolu pomocí van der Waalsových sil. Při vysokých absolutních teplotách (více než 300 K) a nízkých tlacích (méně než jedna atmosféra) je však kinetická energie atomů a molekul mnohem vyšší než energie van der Waalsových interakcí, takže skutečný plyn při uvedenémpodmínky s vysokou přesností lze považovat za ideální.
Boyle-Mariotte rovnice
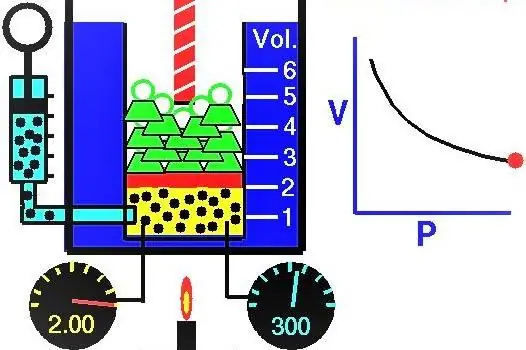
Vlastnosti plynů evropští vědci aktivně zkoumali během XVII-XIX století. Úplně první zákon o plynu, který byl experimentálně objeven, byl zákon popisující izotermické procesy expanze a stlačování plynového systému. Odpovídající experimenty provedli Robert Boyle v roce 1662 a Edm Mariotte v roce 1676. Každý z těchto vědců nezávisle prokázal, že během izotermického procesu v uzavřeném plynovém systému se tlak mění nepřímo s objemem. Experimentálně získané matematické vyjádření procesu je zapsáno v následujícím tvaru:
PV=k
Kde P a V jsou tlak v soustavě a její objem, k je nějaká konstanta, jejíž hodnota závisí na množství plynné látky a její teplotě. Pokud sestavíte závislost funkce P(V) na grafu, bude to hyperbola. Příklad těchto křivek je uveden níže.
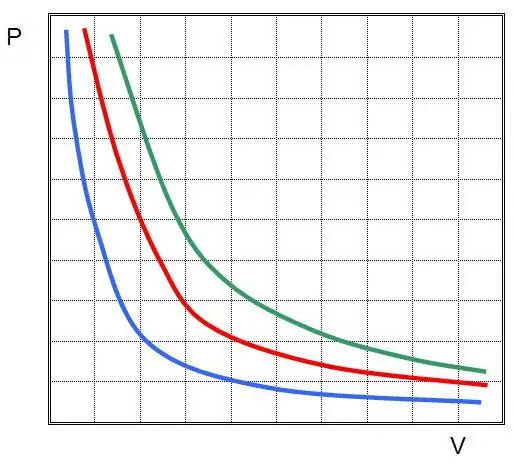
Psaná rovnost se nazývá Boyle-Mariotteova rovnice (zákon). Tento zákon lze stručně formulovat takto: expanze ideálního plynu při konstantní teplotě vede k úměrnému poklesu tlaku v něm, naopak izotermická komprese plynového systému je doprovázena úměrným zvýšením tlaku v něm.
Rovnice ideálního plynu
Boyle-Mariotteův zákon je zvláštním případem obecnějšího zákona, který nese jména Mendělejev aClapeyron. Emile Clapeyron, shrnující experimentální informace o chování plynů za různých vnějších podmínek, získal v roce 1834 následující rovnici:
PV=nRT
Jinými slovy, součin objemu V plynového systému a tlaku P v něm je přímo úměrný součinu absolutní teploty T a látkového množství n. Koeficient této úměrnosti se označuje písmenem R a nazývá se plynová univerzální konstanta. V psané rovnici se hodnota R objevila díky nahrazení řady konstant, které vytvořil Dmitrij Ivanovič Mendělejev v roce 1874.
Z univerzální stavové rovnice je snadné vidět, že stálost teploty a látkové množství zaručuje neměnnost pravé strany rovnice, což znamená, že levá strana rovnice také zůstane konstantní. V tomto případě dostaneme Boyleovu-Mariotteovu rovnici.

Jiné zákony o plynu
Clapeyron-Mendelejevova rovnice napsaná v odstavci výše obsahuje tři termodynamické parametry: P, V a T. Pokud je každý z nich pevný a zbývající dva se mohou měnit, dostaneme Boyle-Mariotte, Charlesova a Gay-Lussacova rovnice. Charlesův zákon hovoří o přímé úměrnosti mezi objemem a teplotou pro izobarický proces a Gay-Lussacův zákon říká, že v případě izochorického přechodu tlak plynu roste nebo klesá přímo úměrně absolutní teplotě. Odpovídající rovnice vypadají takto:
V/T=const, když P=const;
P/T=konst, když V=konst.
TakžeBoyle-Mariottův zákon je tedy jedním ze tří hlavních plynových zákonů. Od ostatních se však liší z hlediska grafické závislosti: funkce V(T) a P(T) jsou přímky, funkce P(V) je hyperbola.
Příklad úlohy pro aplikaci Boyle-Mariotteova zákona
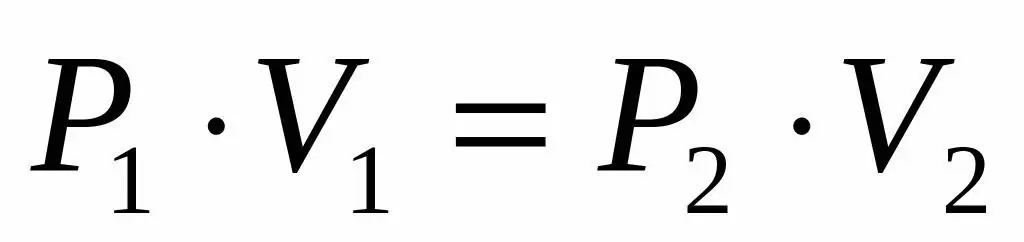
Objem plynu ve válci pod pístem ve výchozí poloze byl 2 litry a jeho tlak byl 1 atmosféra. Jaký byl tlak plynu po zvednutí pístu a zvětšení objemu plynové soustavy o 0,5 litru. Proces je považován za izotermický.
Vzhledem k tomu, že máme dán tlak a objem ideálního plynu a také víme, že teplota zůstává během jeho expanze nezměněna, můžeme použít Boyle-Mariotteovu rovnici v následujícím tvaru:
P1V1=P2V 2
Tato rovnost říká, že součin objem-tlak je konstantní pro každý stav plynu při dané teplotě. Vyjádřením hodnoty P2 z rovnosti získáme konečný vzorec:
P2=P1V1/V 2
Při výpočtech tlaku můžete v tomto případě použít jednotky mimo systém, protože litry se scvrknou a dostaneme tlak P2 v atmosférách. Nahrazením dat z podmínky dospějeme k odpovědi na otázku problému: P2=0,8 atmosféry.






