Ideální plyn, stavová rovnice ideálního plynu, jeho teplota a tlak, objem… ve výčtu parametrů a definic používaných v příslušné části fyziky lze pokračovat ještě dlouho. Dnes budeme mluvit právě na toto téma.
Co se považuje za molekulární fyziku?

Hlavním předmětem zvažovaným v této části je ideální plyn. Stavová rovnice ideálního plynu byla získána s přihlédnutím k normálním podmínkám prostředí a budeme o tom mluvit o něco později. Nyní přistupme k tomuto „problému“z povzdálí.
Řekněme, že máme nějaké množství plynu. Jeho stav lze určit pomocí tří parametrů termodynamického charakteru. Těmi jsou samozřejmě tlak, objem a teplota. Rovnice stavu systému v tomto případě bude vzorcem pro vztah mezi odpovídajícími parametry. Vypadá to takto: F (p, V, T)=0.
Poprvé se zde pomalu blížíme ke vzniku něčeho jako ideálníhoplyn. Říká se mu plyn, ve kterém jsou interakce mezi molekulami zanedbatelné. Obecně to v přírodě neexistuje. Každý vysoce zředěný plyn je mu však blízký. Dusík, kyslík a vzduch, které jsou za normálních podmínek, se jen málo liší od ideálu. K sepsání stavové rovnice pro ideální plyn můžeme použít jednotný zákon o plynu. Dostaneme: pV/T=konst.
Související koncept 1: Avogadrův zákon
Může nám říci, že pokud vezmeme stejný počet molů absolutně libovolného plynu a uvedeme je do stejných podmínek, včetně teploty a tlaku, pak plyny zaberou stejný objem. Konkrétně byl experiment prováděn za normálních podmínek. To znamená, že teplota byla 273,15 Kelvina, tlak jedna atmosféra (760 milimetrů rtuti, neboli 101325 Pascalů). Při těchto parametrech zabíral plyn objem rovný 22,4 litru. Můžeme tedy říci, že pro jeden mol libovolného plynu bude poměr číselných parametrů konstantní hodnotou. Proto bylo rozhodnuto označit tento údaj písmenem R a nazvat jej univerzální plynovou konstantou. Tedy rovná se 8,31. Jednotkou je J/molK.
Ideální plyn. Stavová rovnice ideálního plynu a její manipulace
Zkusme vzorec přepsat. Za tímto účelem jej zapíšeme v tomto tvaru: pV=RT. Dále provedeme jednoduchou akci, vynásobíme obě strany rovnice libovolným počtem molů. Dostaneme pVu=uRT. Vezměme v úvahu skutečnost, že součin molárního objemu amnožství hmoty je jednoduše objem. Ale konec konců bude počet molů současně roven podílu hmotnosti a molární hmotnosti. Přesně tak vypadá Mendělejevova-Clapeyronova rovnice. Dává jasnou představu o tom, jaký druh systému tvoří ideální plyn. Stavová rovnice pro ideální plyn bude mít tvar: pV=mRT/M.
Odvodit vzorec pro tlak
Udělejme další manipulace se získanými výrazy. Za tímto účelem se pravá strana Mendělejevovy-Clapeyronovy rovnice vynásobí a vydělí Avogadrovým číslem. Nyní se pečlivě podíváme na součin množství látky podle Avogadrova čísla. To není nic jiného než celkový počet molekul v plynu. Ale zároveň bude poměr univerzální plynové konstanty k Avogadrově číslu roven Boltzmannově konstantě. Proto mohou být vzorce pro tlak zapsány následovně: p=NkT/V nebo p=nkT. Zde symbol n představuje koncentraci částic.
Procesy ideálního plynu
V molekulární fyzice existuje něco jako izoprocesy. Jedná se o termodynamické procesy, které probíhají v systému při jednom z konstantních parametrů. V tomto případě musí hmotnost látky také zůstat konstantní. Pojďme se na ně podívat konkrétněji. Takže zákony ideálního plynu.
Tlak zůstává konstantní
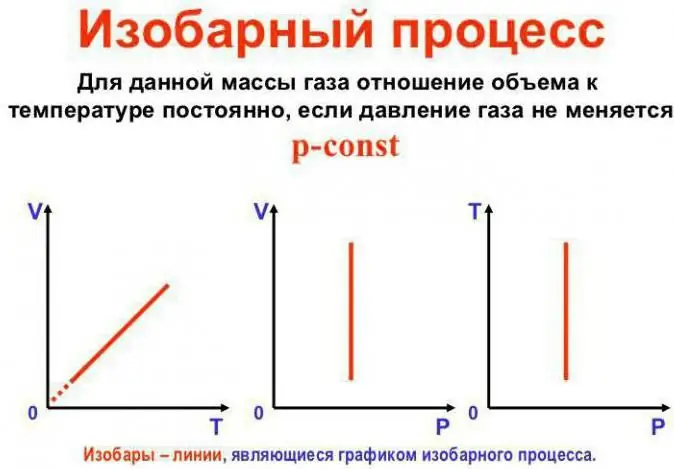
Toto je Gay-Lussacův zákon. Vypadá to takto: V/T=konst. Lze jej přepsat i jiným způsobem: V=Vo (1 + at). Zde a je rovno 1/273,15 K^-1 a nazývá se "koeficient objemové expanze". Teplotu můžeme dosadit jak ve stupních Celsia, tak iKelvinova stupnice. V druhém případě dostaneme vzorec V=Voat.
Hlasitost zůstává konstantní

Toto je druhý Gay-Lussacův zákon, běžněji označovaný jako Charlesův zákon. Vypadá to takto: p/T=konst. Existuje další formulace: p=po (1 + at). Transformace mohou být provedeny v souladu s předchozím příkladem. Jak vidíte, zákony ideálního plynu jsou si někdy dost podobné.
Teplota zůstává konstantní

Pokud teplota ideálního plynu zůstává konstantní, můžeme získat Boyle-Mariotteův zákon. Může být zapsán takto: pV=const.
Související koncept 2: Parciální tlak
Řekněme, že máme nádobu s plyny. Bude to směs. Systém je ve stavu tepelné rovnováhy a samotné plyny spolu nereagují. Zde N bude označovat celkový počet molekul. N1, N2 a tak dále, počet molekul v každé ze složek směsi. Vezměme tlakový vzorec p=nkT=NkT/V. Lze jej otevřít pro konkrétní případ. Pro dvousložkovou směs bude mít vzorec tvar: p=(N1 + N2) kT/V. Pak se ale ukáže, že celkový tlak se bude sčítat z parciálních tlaků každé směsi. Takže to bude vypadat jako p1 + p2 a tak dále. To budou parciální tlaky.
K čemu to je?
Vzorec, který jsme získali, ukazuje, že tlak v systému pochází z každé skupiny molekul. Mimochodem nezávisí naostatní. D alton toho využil při formulování zákona, později po něm pojmenovaného: ve směsi, kde plyny mezi sebou chemicky nereagují, bude celkový tlak roven součtu parciálních tlaků.






