Svět, ve kterém žijeme, je nepředstavitelně krásný a plný mnoha různých procesů, které určují běh života. Všechny tyto procesy studuje známá věda - fyzika. Poskytuje příležitost získat alespoň nějakou představu o původu vesmíru. V tomto článku se budeme zabývat takovým konceptem, jako je molekulární kinetická teorie, její rovnice, typy a vzorce. Než však přistoupíte k hlubšímu studiu těchto problémů, musíte si ujasnit samotný význam fyziky a oblastí, které studuje.
Co je fyzika?

Ve skutečnosti se jedná o velmi rozsáhlou vědu a možná jednu z nejzákladnějších v historii lidstva. Například, pokud je stejná počítačová věda spojena s téměř každou oblastí lidské činnosti, ať už je to počítačový design nebo tvorba karikatur, pak je fyzika život sám, popis jeho složitých procesů a toků. Pokusme se pochopit jeho význam a co nejvíce zjednodušit porozumění.
TakžeFyzika je tedy věda, která se zabývá studiem energie a hmoty, souvislostí mezi nimi, vysvětlením mnoha procesů probíhajících v našem obrovském vesmíru. Molekulárně-kinetická teorie struktury hmoty je jen malou kapkou v moři teorií a odvětví fyziky.
Energie, kterou tato věda podrobně studuje, může být zastoupena v různých formách. Například v podobě světla, pohybu, gravitace, záření, elektřiny a mnoha dalších forem. V tomto článku se dotkneme molekulární kinetické teorie struktury těchto forem.
Studium hmoty nám dává představu o atomové struktuře hmoty. Mimochodem, vyplývá to z molekulárně-kinetické teorie. Nauka o struktuře hmoty nám umožňuje pochopit a najít smysl naší existence, důvody vzniku života i samotného Vesmíru. Zkusme ještě studovat molekulární kinetickou teorii hmoty.
Nejprve je potřeba trochu úvodu, abychom plně porozuměli terminologii a případným závěrům.
Fyzikální témata
Při odpovědi na otázku, co je molekulárně-kinetická teorie, nelze než mluvit o částech fyziky. Každý z nich se zabývá podrobným studiem a vysvětlením konkrétní oblasti lidského života. Jsou klasifikovány takto:
- Mechanika, která je rozdělena do dvou dalších sekcí: kinematika a dynamika.
- Statické.
- Termodynamika.
- Molekulární sekce.
- Elektrodynamika.
- Optika.
- Fyzika kvant a atomového jádra.
Promluvme si konkrétně o molekulárnífyzika, protože je založena na molekulárně-kinetické teorii.
Co je termodynamika?
Obecně platí, že molekulární část a termodynamika jsou úzce související obory fyziky, které studují výhradně makroskopickou složku celkového počtu fyzikálních systémů. Stojí za připomenutí, že tyto vědy přesně popisují vnitřní stav těl a látek. Například jejich stav při zahřívání, krystalizaci, odpařování a kondenzaci, na atomární úrovni. Jinými slovy, molekulární fyzika je věda o systémech, které se skládají z velkého množství částic: atomů a molekul.
Byly to tyto vědy, které studovaly hlavní ustanovení molekulární kinetické teorie.
Ještě v průběhu sedmé třídy jsme se seznamovali s pojmy mikro- a makrosvěty, systémy. Nebude zbytečné obnovovat tyto výrazy v paměti.
Mikrosvět, jak vidíme již z jeho názvu, se skládá z elementárních částic. Jinými slovy, toto je svět malých částic. Jejich velikosti se měří v rozsahu od 10-18 m do 10-4 m a doba jejich skutečného stavu může dosáhnout nekonečna i neúměrně malé intervaly, například 10-20 s.
Makrosvět uvažuje o tělech a systémech stabilních forem, skládajících se z mnoha elementárních částic. Takové systémy jsou úměrné naší lidské velikosti.
Kromě toho existuje něco jako megasvět. Skládá se z obrovských planet, vesmírných galaxií a komplexů.
Základyteorie
Nyní, když jsme si to trochu zrekapitulovali a připomněli si základní pojmy fyziky, můžeme přejít přímo k hlavnímu tématu tohoto článku.
Molekulárně-kinetická teorie se objevila a byla poprvé formulována v devatenáctém století. Jeho podstata spočívá v tom, že podrobně popisuje strukturu jakékoli látky (častěji strukturu plynů než pevných a kapalných těles), na základě tří základních ustanovení, která byla shromážděna z předpokladů tak významných vědců, jako jsou Robert Hooke, Isaac Newton, Daniel Bernoulli, Michail Lomonosov a mnoho dalších.
Hlavní ustanovení molekulární kinetické teorie zní takto:
- Naprosto všechny látky (bez ohledu na to, zda jsou kapalné, pevné nebo plynné) mají složitou strukturu skládající se z menších částic: molekul a atomů. Atomy se někdy nazývají „elementární molekuly“.
- Všechny tyto elementární částice jsou vždy ve stavu nepřetržitého a chaotického pohybu. Každý z nás se setkal s přímým důkazem tohoto tvrzení, ale pravděpodobně mu nepřikládal velký význam. Všichni jsme například na pozadí slunečních paprsků viděli, že částice prachu se neustále pohybují chaotickým směrem. To je způsobeno skutečností, že atomy se vzájemně tlačí a neustále si předávají kinetickou energii. Tento jev byl poprvé studován v roce 1827 a byl pojmenován po objeviteli - „Brownův pohyb“.
- Všechny elementární částice jsou v procesu nepřetržité vzájemné interakceurčité síly, které mají elektrický kámen.
Za zmínku stojí, že dalším příkladem popisujícím polohu číslo dvě, který může platit například i pro molekulární kinetickou teorii plynů, je difúze. Setkáváme se s ním v každodenním životě a při mnoha testech a kontrolách, takže je důležité o tom mít představu.
Nejprve zvažte následující příklady:
Doktor omylem vylil alkohol z láhve na stůl. Nebo jsi možná upustil lahvičku s parfémem a rozlil se po podlaze.
Proč v těchto dvou případech jak vůně alkoholu, tak vůně parfému po nějaké době naplní celou místnost, a nejen oblast, kam se obsah těchto látek rozlil?
Odpověď je jednoduchá: difúze.
Difúze - co to je? Jak to teče?

Jedná se o proces, při kterém částice, které tvoří jednu konkrétní látku (obvykle plyn), pronikají do mezimolekulárních dutin jiné. V našich příkladech výše se stalo následující: v důsledku tepelného, to znamená nepřetržitého a disociovaného pohybu, se molekuly alkoholu a/nebo parfému dostaly do mezer mezi molekulami vzduchu. Postupně se vlivem srážky s atomy a molekulami vzduchu šíří po místnosti. Mimochodem, intenzita difúze, tedy rychlost jejího proudění, závisí na hustotě látek podílejících se na difúzi a také na energii pohybu jejich atomů a molekul, nazývané kinetická. Čím větší je kinetická energie, tím vyšší je rychlost těchto molekul a jejich intenzita.
Nejrychlejší proces difúze lze nazvat difúzí v plynech. To je způsobeno skutečností, že plyn není svým složením homogenní, což znamená, že mezimolekulární dutiny v plynech zabírají značné množství prostoru a proces získávání atomů a molekul cizí látky do nich probíhá snadněji a rychleji..
Tento proces je v kapalinách trochu pomalejší. Rozpouštění kostkového cukru v hrnku čaje je jen příkladem difúze pevné látky v kapalině.
Nejdelší doba je však difúze v tělesech s pevnou krystalickou strukturou. Je to přesně tak, protože struktura pevných látek je homogenní a má silnou krystalovou mřížku, v jejíchž buňkách vibrují atomy pevné látky. Například, pokud jsou povrchy dvou kovových tyčí dobře vyčištěny a poté uvedeny do vzájemného kontaktu, pak po dostatečně dlouhé době budeme schopni detekovat kusy jednoho kovu v druhém a naopak.
Stejně jako každá jiná základní část je základní teorie fyziky rozdělena do samostatných částí: klasifikace, typy, vzorce, rovnice a tak dále. Tak jsme se naučili základy molekulární kinetické teorie. To znamená, že můžete bezpečně přejít k úvahám o jednotlivých teoretických blocích.
Molekulárně-kinetická teorie plynů
Je potřeba porozumět ustanovením plynové teorie. Jak jsme řekli dříve, budeme uvažovat makroskopické charakteristiky plynů, jako je tlak a teplota. Tohle jebude potřeba později k odvození rovnice molekulárně-kinetické teorie plynů. Ale matematika - později, a teď se pojďme zabývat teorií a podle toho fyzikou.
Vědci formulovali pět ustanovení molekulární teorie plynů, která slouží k pochopení kinetického modelu plynů. Znějí takto:
- Všechny plyny se skládají z elementárních částic, které nemají určitou velikost, ale mají určitou hmotnost. Jinými slovy, objem těchto částic je minimální ve srovnání s délkou mezi nimi.
- Atomy a molekuly plynů nemají prakticky žádnou potenciální energii, respektive podle zákona je veškerá energie rovna kinetické.
- S touto pozicí jsme se již seznámili dříve - Brownův pohyb. To znamená, že částice plynu jsou vždy v nepřetržitém a chaotickém pohybu.
- Naprosto všechny vzájemné srážky částic plynu, doprovázené poselstvím rychlosti a energie, jsou zcela elastické. To znamená, že během srážky nedochází k žádné ztrátě energie ani prudkým skokům v jejich kinetické energii.
- Za normálních podmínek a konstantní teploty je průměrná energie pohybu částic téměř všech plynů stejná.
Pátou pozici můžeme přepsat tímto typem rovnice molekulárně-kinetické teorie plynů:
E=1/2mv^2=3/2kT, kde k je Boltzmannova konstanta; T - teplota v Kelvinech.
Tato rovnice nám umožňuje pochopit vztah mezi rychlostí elementárních částic plynu a jejich absolutní teplotou. V souladu s tím, čím vyšší je jejich absolutníteplota, tím větší je jejich rychlost a kinetická energie.
Tlak plynu
Takové makroskopické složky charakteristiky, jako je tlak plynů, lze také vysvětlit pomocí kinetické teorie. K tomu si představme následující příklad.
Předpokládejme, že molekula nějakého plynu je v krabici, jejíž délka je L. Využijme ustanovení plynové teorie popsané výše a vezměme v úvahu skutečnost, že molekulární koule se pohybuje pouze po x -osa. Budeme tak moci pozorovat proces pružné srážky s jednou ze stěn nádoby (krabice).
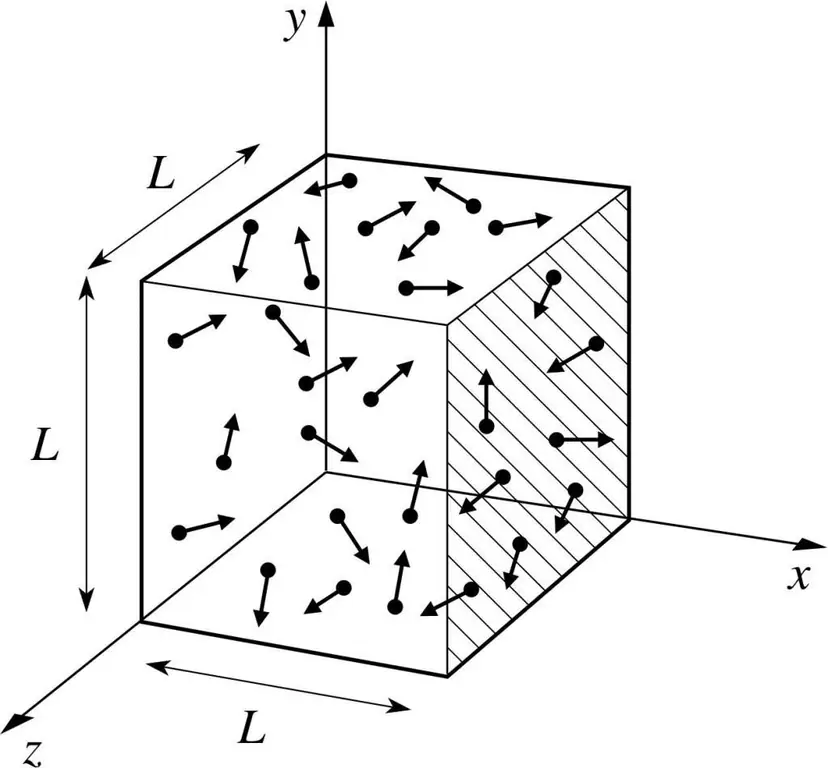
Hybnost probíhající kolize, jak víme, je určena vzorcem: p=mv, ale v tomto případě bude mít tento vzorec tvar projekce: p=mv(x).
Jelikož uvažujeme pouze rozměr osy x, tedy osy x, bude celková změna hybnosti vyjádřena vzorcem: mv(x) - m(-v(x))=2mv(x).
Dále zvažte sílu vyvíjenou naším objektem pomocí druhého Newtonova zákona: F=ma=P/t.
Z těchto vzorců vyjádříme tlak ze strany plynu: P=F/a;
Nyní dosadíme silový výraz do výsledného vzorce a dostaneme: P=mv(x)^2/L^3.
Poté může být náš hotový tlakový vzorec zapsán pro N-tý počet molekul plynu. Jinými slovy, bude to vypadat takto:
P=Nmv(x)^2/V, kde v je rychlost a V je hlasitost.
Nyní se pokusíme zdůraznit několik základních ustanovení o tlaku plynu:
- Projevuje se prostřednictvímsrážky molekul s molekulami stěn objektu, ve kterém se nachází.
- Velikost tlaku je přímo úměrná síle a rychlosti dopadu molekul na stěny nádoby.
Několik stručných závěrů k teorii
Než půjdeme dále a zvážíme základní rovnici molekulární kinetické teorie, nabízíme vám několik stručných závěrů z výše uvedených bodů a teorie:
- Mírou průměrné energie pohybu jejích atomů a molekul je absolutní teplota.
- Když mají dva různé plyny stejnou teplotu, jejich molekuly mají stejnou průměrnou kinetickou energii.
- Energie částic plynu je přímo úměrná střední čtvercové rychlosti: E=1/2mv^2.
- Přestože molekuly plynu mají průměrnou kinetickou energii a průměrnou rychlost, jednotlivé částice se pohybují různými rychlostmi: některé rychle, některé pomalu.
- Čím vyšší teplota, tím vyšší rychlost molekul.
- Kolikrát zvýšíme teplotu plynu (například dvojnásobně), tolikrát se zvýší energie pohybu jeho částic (respektive dvojnásobně).
Základní rovnice a vzorce

Základní rovnice molekulární kinetické teorie umožňuje stanovit vztah mezi veličinami mikrosvěta a tedy makroskopickými, tedy měřenými veličinami.
Jeden z nejjednodušších modelů, které může molekulární teorie zvážit, je model ideálního plynu.
Dalo by se to tak řícttoto je druh imaginárního modelu studovaného molekulární kinetickou teorií ideálního plynu, ve kterém:
- nejjednodušší částice plynu jsou považovány za dokonale elastické koule, které interagují jak mezi sebou, tak s molekulami stěn jakékoli nádoby pouze v jednom případě - absolutně elastická srážka;
- přitažlivé síly uvnitř plynu chybí nebo je lze ve skutečnosti zanedbat;
- prvky vnitřní struktury plynu lze brát jako hmotné body, to znamená, že jejich objem lze také zanedbat.
S ohledem na takový model sepsal fyzik německého původu Rudolf Clausius vzorec pro tlak plynu prostřednictvím vztahu mikroskopických a makroskopických parametrů. Vypadá to takto:
p=1/3m(0)nv^2.
Tento vzorec bude později nazýván jako základní rovnice molekulárně-kinetické teorie ideálního plynu. Může být prezentován v několika různých formách. Naší povinností je nyní ukázat sekce jako molekulární fyzika, molekulární kinetická teorie, a tedy jejich kompletní rovnice a typy. Proto má smysl uvažovat o dalších variantách základního vzorce.
Víme, že průměrnou energii charakterizující pohyb molekul plynu lze nalézt pomocí vzorce: E=m(0)v^2/2.
V tomto případě můžeme nahradit výraz m(0)v^2 v původním tlakovém vzorci průměrnou kinetickou energií. V důsledku toho budeme mít příležitost sestavit základní rovnici molekulární kinetické teorie plynů v následujícím tvaru: p=2/3nE.
Kromě toho všichni víme, že výraz m(0)n lze zapsat jako součin dvou kvocientů:
m/NN/V=m/V=ρ.
Po těchto manipulacích můžeme přepsat náš vzorec pro rovnici molekulárně-kinetické teorie ideálního plynu ve třetí, odlišné formě:
p=1/3ρv^2.
No, to je možná vše, co o tomto tématu potřebujete vědět. Zbývá pouze systematizovat získané poznatky ve formě stručných (a nikoli tak) závěrů.
Všechny obecné závěry a vzorce na téma "Molekulárně kinetická teorie"
Tak pojďme začít.
První:
Fyzika je základní věda zahrnutá do kurzu přírodních věd, která studuje vlastnosti hmoty a energie, jejich strukturu, vzorce anorganické přírody.
Zahrnuje následující sekce:
- mechanika (kinematika a dynamika);
- static;
- termodynamika;
- elektrodynamika;
- molekulární sekce;
- optika;
- fyzika kvant a atomového jádra.
Druhý:
Fyzika částic a termodynamika jsou úzce související obory, které studují výhradně makroskopickou složku celkového počtu fyzikálních systémů, tedy systémy sestávající z obrovského množství elementárních částic.
Jsou založeny na molekulární kinetické teorii.
Třetí:
Podstatou věci je toto. Molekulární kinetická teorie podrobně popisuje strukturu látky (častěji strukturu plynů než pevných látek).a tekutá těla), založené na třech základních předpokladech, které byly shromážděny z předpokladů předních vědců. Mezi nimi: Robert Hooke, Isaac Newton, Daniel Bernoulli, Michail Lomonosov a mnoho dalších.
Čtvrtý:
Tři základní principy molekulární kinetické teorie:
- Všechny látky (bez ohledu na to, zda jsou kapalné, pevné nebo plynné) mají složitou strukturu skládající se z menších částic: molekul a atomů.
- Všechny tyto jednoduché částice jsou v nepřetržitém chaotickém pohybu. Příklad: Brownův pohyb a difúze.
- Všechny molekuly za jakýchkoli podmínek na sebe vzájemně působí určitými silami, které mají elektrický kámen.
Každé z těchto ustanovení molekulární kinetické teorie je pevným základem pro studium struktury hmoty.
Pátý:
Několik hlavních bodů molekulární teorie pro model plynu:
- Všechny plyny se skládají z elementárních částic, které nemají určitou velikost, ale mají určitou hmotnost. Jinými slovy, objem těchto částic je minimální ve srovnání se vzdálenostmi mezi nimi.
- Atomy a molekuly plynů nemají prakticky žádnou potenciální energii, respektive jejich celková energie je rovna kinetické.
- S touto pozicí jsme se již seznámili dříve - Brownův pohyb. To znamená, že částice plynu jsou vždy v nepřetržitém a náhodném pohybu.
- Naprosto všechny vzájemné srážky atomů a molekul plynů, doprovázené poselstvím rychlosti a energie, jsou zcela elastické. Tohle jeznamená, že během srážky nedochází k žádné ztrátě energie nebo prudkým skokům v jejich kinetické energii.
- Za normálních podmínek a konstantní teploty je průměrná kinetická energie téměř všech plynů stejná.
Šestý:
Závěry z teorie o plynech:
- Absolutní teplota je mírou průměrné kinetické energie jejích atomů a molekul.
- Když mají dva různé plyny stejnou teplotu, jejich molekuly mají stejnou průměrnou kinetickou energii.
- Průměrná kinetická energie částic plynu je přímo úměrná střední kvadratické rychlosti: E=1/2mv^2.
- Přestože molekuly plynu mají průměrnou kinetickou energii a průměrnou rychlost, jednotlivé částice se pohybují různými rychlostmi: některé rychle, některé pomalu.
- Čím vyšší teplota, tím vyšší rychlost molekul.
- Kolikrát zvýšíme teplotu plynu (například dvojnásobně), tolikrát se také zvýší průměrná kinetická energie jeho částic (respektive dvojnásobně).
- Vztah mezi tlakem plynu na stěnách nádoby, ve které se nachází, a intenzitou dopadů molekul na tyto stěny je přímo úměrný: čím více dopadů, tím vyšší tlak a naopak.
Sedmé:
Ideální model plynu je model, ve kterém musí být splněny následující podmínky:
- Molekuly plynu mohou a jsou považovány za dokonale elastické kuličky.
- Tyto koule mohou interagovat mezi sebou a se stěnami libovolnéhoplavidlo pouze v jednom případě - absolutně elastická kolize.
- Síly, které popisují vzájemný tah mezi atomy a molekulami plynu chybí nebo je lze ve skutečnosti zanedbat.
- Atomy a molekuly jsou považovány za hmotné body, to znamená, že jejich objem lze také zanedbat.
Osmý:
Uveďme všechny základní rovnice a ukažme vzorce v tématu "Molekulárně kinetická teorie":
p=1/3m(0)nv^2 - základní rovnice pro model ideálního plynu, odvozená německým fyzikem Rudolfem Clausiem.
p=2/3nE - základní rovnice molekulárně-kinetické teorie ideálního plynu. Odvozeno z průměrné kinetické energie molekul.
р=1/3ρv^2 - stejná rovnice, ale uvažována prostřednictvím hustoty a střední kvadratické rychlosti molekul ideálního plynu.
m(0)=M/N(a) - vzorec pro zjištění hmotnosti jedné molekuly prostřednictvím Avogadroova čísla.
v^2=(v(1)+v(2)+v(3)+…)/N - vzorec pro zjištění střední kvadratické rychlosti molekul, kde v(1), v(2), v (3) a tak dále - rychlost první molekuly, druhé, třetí a tak dále až po n-tou molekulu.
n=N/V - vzorec pro zjištění koncentrace molekul, kde N je počet molekul v objemu plynu k danému objemu V.
E=mv^2/2=3/2kT - vzorce pro zjištění průměrné kinetické energie molekul, kde v^2 je střední kvadratická rychlost molekul, k je konstanta hodnota pojmenovaná po rakouské fyzice Ludwiga Boltzmanna a T je teplota plynu.
p=nkT - tlakový vzorec z hlediska koncentrace, konstantníBoltzmann a absolutní teplota T. Z toho vyplývá další základní vzorec, který objevili ruský vědec Mendělejev a francouzský fyzik-inženýr Claiperon:
pV=m/MRT, kde R=kN(a) je univerzální konstanta pro plyny.
Nyní si ukážeme konstanty pro různé izoprocesy: izobarické, izochorické, izotermické a adiabatické.
pV/T=const - provádí se, když je hmotnost a složení plynu konstantní.
рV=konst - pokud je také konstantní teplota.
V/T=konst - pokud je tlak plynu konstantní.
p/T=const - pokud je objem konstantní.
To je možná vše, co potřebujete k tomuto tématu vědět.
Dnes jsme se vrhli do takového vědeckého oboru, jakým je teoretická fyzika, její četné sekce a bloky. Podrobněji jsme se dotkli takové oblasti fyziky, jako je základní molekulární fyzika a termodynamika, konkrétně molekulárně-kinetická teorie, která, jak se zdá, nepředstavuje žádné potíže v počáteční studii, ale ve skutečnosti má mnoho úskalí.. Rozšiřuje naše chápání modelu ideálního plynu, který jsme také podrobně studovali. Kromě toho stojí za zmínku, že jsme se také seznámili se základními rovnicemi molekulární teorie v jejich různých obměnách a také zvážili všechny nejnutnější vzorce pro zjištění určitých neznámých veličin na toto téma. To se bude hodit zejména při přípravě na psaní jakékoli testy, zkoušky a testy nebo k rozšíření obecného rozhledu a znalostí fyziky.
Doufáme, že pro vás byl tento článek užitečný a že jste z něj získali jen ty nejnutnější informace, které posílí vaše znalosti v takových pilířích termodynamiky, jako jsou základní ustanovení molekulární kinetické teorie.






