Existují předměty, které jsou schopny měnit hustotu toku elektromagnetického záření, které na ně dopadá, to znamená buď ji zvětšovat tím, že ji shromažďuje v jednom bodě, nebo ji zmenšovat jejím rozptylem. Tyto objekty se ve fyzice nazývají čočky. Pojďme se na tento problém podívat blíže.
Co jsou čočky ve fyzice?
Tento pojem znamená naprosto jakýkoli předmět, který je schopen změnit směr šíření elektromagnetického záření. Toto je obecná definice čoček ve fyzice, která zahrnuje optické brýle, magnetické a gravitační čočky.
V tomto článku se zaměříme na optická skla, což jsou předměty vyrobené z průhledného materiálu a ohraničené dvěma povrchy. Jeden z těchto povrchů musí mít nutně zakřivení (tj. být součástí koule o konečném poloměru), jinak objekt nebude mít vlastnost měnit směr šíření světelných paprsků.
Princip čočky

Podstata práce tohoto nekomplikovanéhooptický objekt je jev lomu slunečních paprsků. Na počátku 17. století publikoval slavný holandský fyzik a astronom Willebrord Snell van Rooyen zákon lomu, který v současnosti nese jeho příjmení. Formulace tohoto zákona je následující: když sluneční světlo prochází rozhraním mezi dvěma opticky průhlednými prostředími, pak součin sinusu úhlu dopadu mezi paprskem a normálou k povrchu a indexu lomu prostředí, ve kterém šíří je konstantní hodnota.

Pro objasnění výše uvedeného uveďme příklad: nechte světlo dopadat na hladinu vody, přičemž úhel mezi normálou k hladině a paprskem je θ1. Poté se světelný paprsek láme a začíná se šířit ve vodě již pod úhlem θ2 k normále k povrchu. Podle Snellova zákona dostáváme: sin(θ1)n1=sin(θ2) n2, kde n1 a n2 jsou indexy lomu vzduchu a vody, resp. Jaký je index lomu? Toto je hodnota, která ukazuje, kolikrát je rychlost šíření elektromagnetických vln ve vakuu větší než u opticky transparentního prostředí, tedy n=c/v, kde c a v jsou rychlosti světla ve vakuu a v střední, respektive.
Fyzika vzhledu lomu spočívá v implementaci Fermatova principu, podle kterého se světlo pohybuje tak, aby překonalo vzdálenost z jednoho bodu do druhého v prostoru v co nejkratším čase.
Typy čoček

Typ optické čočky ve fyzice je určen výhradně tvarem povrchů, které ji tvoří. Na tomto tvaru závisí směr lomu paprsku dopadajícího na ně. Pokud je tedy zakřivení povrchu kladné (konvexní), pak se po výstupu z čočky bude světelný paprsek šířit blíže k její optické ose (viz níže). Naopak, je-li zakřivení povrchu záporné (konkávní), paprsek se při průchodu optickým sklem vzdálí od své středové osy.
Všimněte si znovu, že povrch jakéhokoli zakřivení láme paprsky stejným způsobem (podle Stellova zákona), ale normály k nim mají jiný sklon vzhledem k optické ose, což má za následek odlišné chování lomeného paprsku.
Čočka ohraničená dvěma konvexními plochami se nazývá konvergující čočka. Pokud je zase tvořen dvěma povrchy s negativním zakřivením, nazývá se rozptyl. Všechny ostatní typy optických skel jsou spojeny s kombinací těchto povrchů, ke kterým se přidává i rovina. Jakou vlastnost bude mít kombinovaná čočka (divergentní nebo konvergující) závisí na celkovém zakřivení poloměrů jejích povrchů.
Prvky čočky a vlastnosti paprsku

Abyste mohli zabudovat čočky do fyziky obrazu, musíte se seznámit s prvky tohoto objektu. Jsou uvedeny níže:
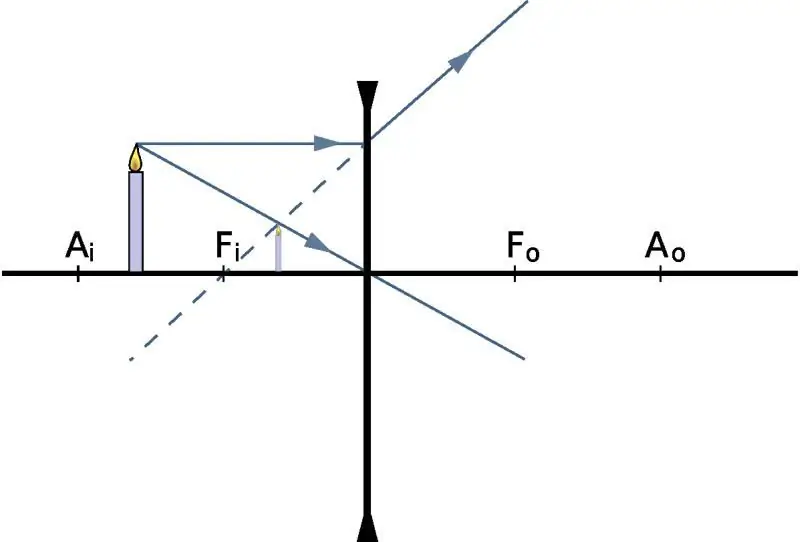
- Hlavní optická osa a střed. V prvním případě znamenají přímku procházející kolmo k čočce jejím optickým středem. Ten je zase bodem uvnitř čočky, kterým paprsek neprochází lomem.
- Ohnisková vzdálenost a ohnisko - vzdálenost mezi středem a bodem na optické ose, který shromažďuje všechny paprsky dopadající na čočku rovnoběžně s touto osou. Tato definice platí pro sběr optických brýlí. V případě divergentních čoček se do bodu nebudou sbíhat samotné paprsky, ale jejich pomyslné pokračování. Tento bod se nazývá hlavní zaměření.
- Optický výkon. Toto je název převrácené hodnoty ohniskové vzdálenosti, to znamená D \u003d 1 / f. Měří se v dioptriích (dioptriích), tedy 1 dioptrii.=1 m-1.
Níže jsou uvedeny hlavní vlastnosti paprsků, které procházejí čočkou:
- paprsek procházející optickým středem nemění směr svého pohybu;
- paprsky dopadající rovnoběžně s hlavní optickou osou mění svůj směr tak, že procházejí hlavním ohniskem;
- paprsky dopadající na optické sklo pod libovolným úhlem, ale procházející jeho ohniskem, mění svůj směr šíření tak, že se stávají rovnoběžnými s hlavní optickou osou.
Výše uvedené vlastnosti paprsků pro tenké čočky ve fyzice (jak se jim říká, protože bez ohledu na to, jaké koule jsou tvořeny a jak jsou tlusté, záleží pouze na optických vlastnostech předmětu) se používají k vytváření obrazů v nich.
Obrázky v optických brýlích: jak postavit?
Níže je obrázek, který podrobně popisuje schémata pro konstrukci obrázků v konvexních a konkávních čočkách objektu(červená šipka) v závislosti na jeho poloze.
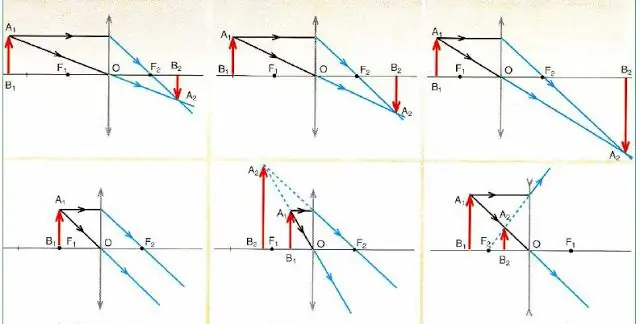
Z analýzy obvodů na obrázku vyplývají důležité závěry:
- Každý obraz je postaven pouze na 2 paprscích (procházejících středem a rovnoběžné s hlavní optickou osou).
- Spojné čočky (označené šipkami na koncích směřujícími ven) mohou poskytnout jak zvětšený, tak zmenšený obraz, který zase může být skutečný (skutečný) nebo imaginární.
- Pokud je objekt zaostřený, pak čočka nevytváří jeho obraz (viz spodní diagram vlevo na obrázku).
- Rozptylové optické brýle (označené šipkami na jejich koncích směřujícími dovnitř) vždy poskytují zmenšený a virtuální obraz bez ohledu na polohu objektu.
Nalezení vzdálenosti k obrázku
Abychom určili, v jaké vzdálenosti se obraz objeví, když známe polohu samotného objektu, použijeme fyzikální vzorec pro čočku: 1/f=1/do + 1 /d i, kde do a di jsou vzdálenost k objektu a k jeho obrazu z optiky střed, respektive f je hlavní ohnisko. Pokud mluvíme o sběrném optickém skle, pak bude f-číslo kladné. Naopak pro divergentní čočku je f záporné.
Použijme tento vzorec a vyřešme jednoduchý problém: nechť je objekt ve vzdálenosti do=2f od středu sběrného optického skla. Kde se objeví jeho obrázek?
Z podmínek problému máme: 1/f=1/(2f)+1/di. Od: 1/di=1/f - 1/(2f)=1/(2f), tj. di=2 F. Obraz se tedy objeví ve vzdálenosti dvou ohnisek od čočky, ale na druhé straně než samotný objekt (to je označeno kladným znaménkem hodnoty di).
Stručná historie
Je zajímavé uvést etymologii slova „čočka“. Pochází z latinských slov lens a lentis, což znamená „čočka“, protože optické objekty svým tvarem skutečně vypadají jako plody této rostliny.
Síla lomu sférických průhledných těles byla známá již starým Římanům. K tomuto účelu používali kulaté skleněné nádoby naplněné vodou. Samotné skleněné čočky se v Evropě začaly vyrábět až ve 13. století. Používaly se jako nástroj pro čtení (moderní brýle nebo lupa).
Aktivní používání optických objektů při výrobě dalekohledů a mikroskopů sahá až do 17. století (na začátku tohoto století Galileo vynalezl první dalekohled). Všimněte si, že matematická formulace Stellova zákona lomu, bez jehož znalosti není možné vyrobit čočky s požadovanými vlastnostmi, byla publikována holandským vědcem na začátku téhož 17. století.
Jiné objektivy
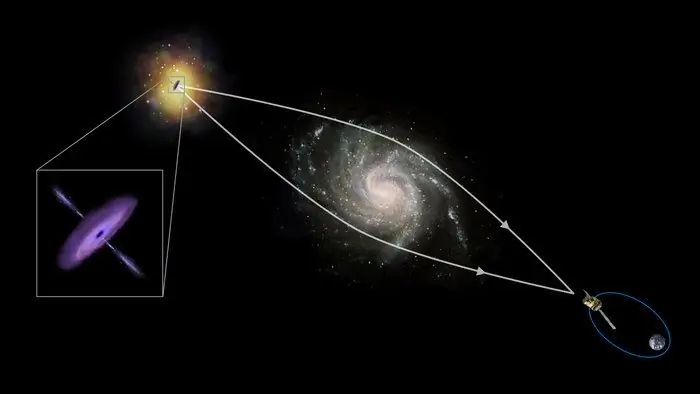
Jak je uvedeno výše, kromě optických refrakčních objektů existují také magnetické a gravitační objekty. Příkladem prvního jsou magnetické čočky v elektronovém mikroskopu, názorným příkladem druhého je zkreslení směru světelného toku,když prochází blízko masivních vesmírných těles (hvězdy, planety).






