Studium procesů probíhajících ve statistických systémech komplikuje minimální velikost částic a jejich obrovský počet. Je prakticky nemožné uvažovat každou částici samostatně, proto se zavádějí statistické veličiny: průměrná rychlost částic, jejich koncentrace, hmotnost částic. Vzorec, který charakterizuje stav systému s přihlédnutím k mikroskopickým parametrům, se nazývá základní rovnice molekulárně-kinetické teorie plynů (MKT).
Něco málo o průměrné rychlosti částic
Stanovení rychlosti částic bylo nejprve provedeno experimentálně. Známý experiment ze školních osnov, který provedl Otto Stern, umožnil vytvořit představu o rychlostech částic. Během experimentu byl studován pohyb atomů stříbra v rotujících válcích: nejprve ve stacionárním stavu zařízení a poté, když se otáčí určitou úhlovou rychlostí.
V důsledku toho bylo zjištěno, že rychlost molekul stříbra přesahuje rychlost zvuku a je 500 m/s. Skutečnost je docela zajímavá, protože pro člověka je obtížné cítit takové rychlosti pohybu částic v látkách.
Ideální plyn
Pokračovat ve výzkumuZdá se to možné pouze v systému, jehož parametry lze určit přímým měřením pomocí fyzikálních přístrojů. Rychlost se měří rychloměrem, ale myšlenka připojení rychloměru k jedné částici je absurdní. Přímo lze měřit pouze makroskopický parametr spojený s pohybem částic.
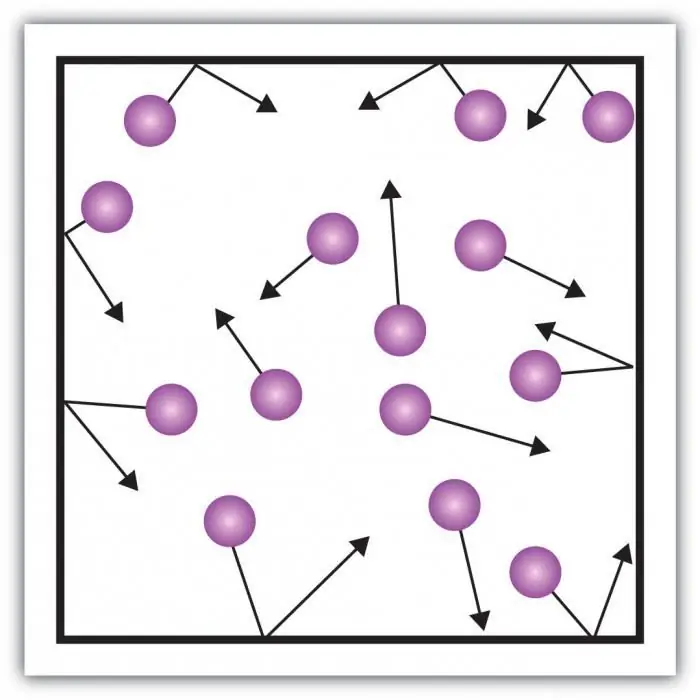
Zvažte tlak plynu. Tlak na stěny nádoby vzniká nárazy molekul plynu v nádobě. Zvláštností plynného skupenství hmoty jsou dostatečně velké vzdálenosti mezi částicemi a jejich malá vzájemná interakce. To vám umožní přímo měřit jeho tlak.
Jakýkoli systém interagujících těles je charakterizován potenciální energií a kinetickou energií pohybu. Skutečný plyn je složitý systém. Variabilita potenciální energie se nehodí k systematizaci. Problém lze vyřešit zavedením modelu, který nese charakteristické vlastnosti plynu, čímž se zamete složitost interakce.
Ideální plyn je stav hmoty, ve kterém je interakce částic zanedbatelná, potenciální energie interakce má tendenci k nule. Za významnou lze považovat pouze energii pohybu, která závisí na rychlosti částic.
Ideální tlak plynu
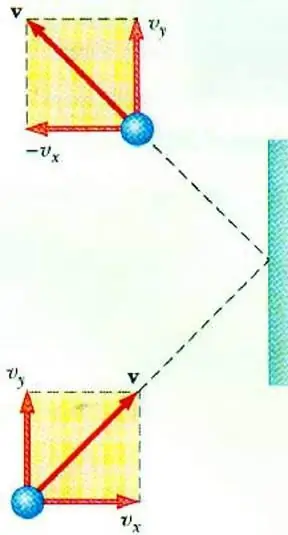
Odhalit vztah mezi tlakem plynu a rychlostí jeho částic umožňuje základní rovnice MKT ideálního plynu. Částice pohybující se v nádobě při dopadu na stěnu jí předá impuls, jehož hodnotu lze určit na základě druhého zákonaNewton:
F∆t=2 m0vx
Změna hybnosti částice při pružném nárazu je spojena se změnou horizontální složky její rychlosti. F je síla působící ze strany částice na stěnu po krátkou dobu t; m0 - hmotnost částic.
Všechny částice plynu se srazí s povrchem oblasti S během doby ∆t, pohybují se ve směru k povrchu rychlostí vx a nacházejí se ve válci o objemu Sυ x Δt. Při koncentraci částic n se přesně polovina molekul pohybuje směrem ke stěně, druhá polovina se pohybuje v opačném směru.
Po zvážení srážky všech částic můžeme napsat Newtonův zákon pro sílu působící na plochu:
F∆t=nm0vx2S∆t
Vzhledem k tomu, že tlak plynu je definován jako poměr síly působící kolmo k povrchu k jeho ploše, můžeme napsat:
p=F: S=nm0vx2
Výsledný vztah jako základní rovnice MKT nemůže popsat celý systém, protože je uvažován pouze jeden směr pohybu.
Distribuce Maxwell
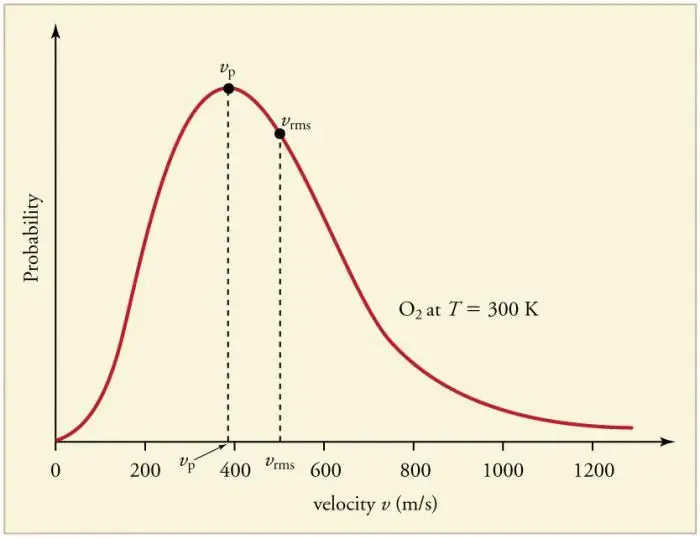
Nepřetržité časté srážky částic plynu se stěnami a mezi sebou navzájem vedou k ustavení určitého statistického rozložení částic z hlediska rychlostí (energií). Směry všech vektorů rychlosti se ukazují jako stejně pravděpodobné. Toto rozdělení se nazývá Maxwellovo rozdělení. V roce 1860 byl tento vzorodvozené J. Maxwellem na základě MKT. Hlavní parametry distribučního zákona se nazývají rychlosti: pravděpodobné, odpovídající maximální hodnotě křivky, a odmocnina vkv=√‹v2 › - střední čtverec rychlosti částice.
Zvýšení teploty plynu odpovídá zvýšení rychlosti.
Na základě skutečnosti, že všechny rychlosti jsou stejné a jejich moduly mají stejnou hodnotu, můžeme předpokládat:
‹v2›=‹vx2› + ‹v y2› + ‹vz2›, od: ‹ vx2›=‹v2›: 3
Základní rovnice MKT, která bere v úvahu průměrnou hodnotu tlaku plynu, je:
p=nm0‹v2›: 3.
Tento vztah je jedinečný v tom, že určuje vztah mezi mikroskopickými parametry: rychlostí, hmotností částic, koncentrací částic a tlakem plynu obecně.
Použitím konceptu kinetické energie částic lze základní rovnici MKT přepsat jinak:
p=2nm0‹v2›: 6=2n‹Ek›: 3
Tlak plynu je úměrný průměrné hodnotě kinetické energie jeho částic.
Teplota
Zajímavé je, že pro konstantní množství plynu v uzavřené nádobě lze uvést do vztahu tlak plynu a průměrnou hodnotu energie pohybu částic. V tomto případě lze tlak měřit měřením energiečástice.
Co dělat? Jakou hodnotu lze srovnat s kinetickou energií? Teplota se ukáže jako taková hodnota.

Teplota je měřítkem tepelného stavu látek. K jejímu měření se používá teploměr, jehož základem je tepelná roztažnost pracovní tekutiny (líh, rtuť) při zahřátí. Stupnice teploměru je vytvořena experimentálně. Obvykle jsou na něm umístěny značky odpovídající poloze pracovní tekutiny při nějakém fyzikálním procesu probíhajícím za konstantního tepelného stavu (vařící voda, tající led). Různé teploměry mají různé stupnice. Například Celsius, Fahrenheit.

Univerzální teplotní stupnice
Plynové teploměry lze považovat za zajímavější z hlediska nezávislosti na vlastnostech pracovní tekutiny. Jejich rozsah nezávisí na druhu použitého plynu. V takovém zařízení lze hypoteticky určit teplotu, při které má tlak plynu tendenci k nule. Výpočty ukazují, že tato hodnota odpovídá -273,15 oC. Teplotní stupnice (absolutní teplotní stupnice nebo Kelvinova stupnice) byla zavedena v roce 1848. Jako hlavní bod této stupnice byla vzata možná teplota nulového tlaku plynu. Jednotkový segment stupnice se rovná jednotkové hodnotě stupnice Celsia. Při studiu plynových procesů se zdá pohodlnější zapsat základní rovnici MKT pomocí teploty.
Vztah mezi tlakem a teplotou
Empiricky si to můžete ověřitúměrnost tlaku plynu jeho teplotě. Zároveň bylo zjištěno, že tlak je přímo úměrný koncentraci částic:
P=nkT,
kde T je absolutní teplota, k je konstanta rovna 1,38•10-23J/K.
Základní hodnota, která má konstantní hodnotu pro všechny plyny, se nazývá Boltzmannova konstanta.
Porovnáním závislosti tlaku na teplotě a základní rovnice plynů MKT můžeme napsat:
‹Ek›=3 kT: 2
Průměrná hodnota kinetické energie pohybu molekul plynu je úměrná jeho teplotě. To znamená, že teplota může sloužit jako míra kinetické energie pohybu částic.






