Přírodní jevy a procesy kolem nás jsou poměrně složité. Pro jejich přesný fyzikální popis je třeba použít těžkopádný matematický aparát a vzít v úvahu velké množství významných faktorů. Aby se tomuto problému předešlo, používají se ve fyzice některé zjednodušené modely, které značně usnadňují matematickou analýzu procesu, ale prakticky neovlivňují přesnost jeho popisu. Jedním z nich je model ideálního plynu. Podívejme se na to podrobněji v článku.
Koncept ideálního plynu
Ideální plyn je stav agregace látky, která se skládá z hmotných bodů, které spolu neinteragují. Pojďme si tuto definici vysvětlit podrobněji.
Za prvé, mluvíme o hmotných bodech jako o objektech, které tvoří ideální plyn. To znamená, že jeho molekuly a atomy nemají velikost, ale mají určitou hmotnost. Je to odvážnéaproximaci lze provést s přihlédnutím ke skutečnosti, že ve všech skutečných plynech při nízkých tlacích a vysokých teplotách je vzdálenost mezi molekulami mnohem větší než jejich lineární rozměry.
Za druhé, molekuly v ideálním plynu by spolu neměly interagovat. Ve skutečnosti takové interakce vždy existují. Takže i atomy vzácných plynů zažívají dipól-dipólovou přitažlivost. Jinými slovy, van der Waalsovy interakce jsou přítomny. Ve srovnání s kinetickou energií rotace a translačního pohybu molekul jsou však tyto interakce tak malé, že neovlivňují vlastnosti plynů. Proto je nelze brát v úvahu při řešení praktických problémů.
Je důležité si uvědomit, že ne všechny plyny s nízkou hustotou a vysokou teplotou lze považovat za ideální. Kromě van der Waalsových interakcí existují další, silnější typy vazeb, například vodíkové vazby mezi molekulami H2O, které vedou k hrubému porušení podmínek ideálního plynu. Z tohoto důvodu není ideální plyn vodní pára, ale vzduch ano.
Fyzikální model ideálního plynu
Tento model lze znázornit následovně: předpokládejme, že plynový systém obsahuje N částic. Mohou to být atomy a molekuly různých chemikálií a prvků. Počet N částic je velký, proto se k jeho popisu obvykle používá jednotka „mol“(1 mol odpovídá Avogadrově číslu). Všechny se pohybují v určitém objemu V. Pohyby částicjsou chaotické a na sobě nezávislé. Každý z nich má určitou rychlost v a pohybuje se po přímé dráze.
Teoreticky je pravděpodobnost srážky mezi částicemi téměř nulová, protože jejich velikost je malá ve srovnání se vzdálenostmi mezi částicemi. Pokud však k takové srážce dojde, pak je absolutně elastická. V druhém případě je zachována celková hybnost částic a jejich kinetická energie.
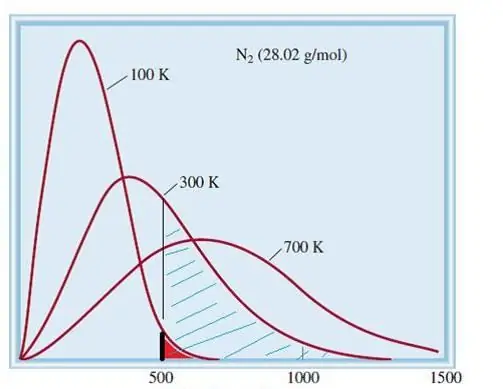
Uvažovaným modelem ideálních plynů je klasický systém s velkým množstvím prvků. Proto se rychlost a energie částic v něm řídí statistickým rozdělením Maxwell-Boltzmanna. Některé částice mají nízké rychlosti, zatímco jiné mají vysoké rychlosti. V tomto případě existuje určitý úzký rychlostní limit, ve kterém leží nejpravděpodobnější hodnoty této veličiny. Distribuce rychlosti molekul dusíku je schematicky znázorněna níže.
Kinetická teorie plynů
Výše popsaný model ideálních plynů jednoznačně určuje vlastnosti plynů. Tento model poprvé navrhl Daniel Bernoulli v roce 1738.

Následně jej do dnešního stavu vyvinuli August Kroenig, Rudolf Clausius, Michail Lomonosov, James Maxwell, Ludwig Boltzmann, Marian Smoluchowski a další vědci.
Kinetická teorie tekutých látek, na jejímž základě je postaven model ideálního plynu, vysvětluje dvě důležité makroskopické vlastnosti systému založené na jeho mikroskopickém chování:
- Tlak v plynech je výsledkem srážky částic se stěnami nádoby.
- Teplota v systému je výsledkem projevu neustálého pohybu molekul a atomů.
Rozšíříme oba závěry kinetické teorie.
Tlak plynu
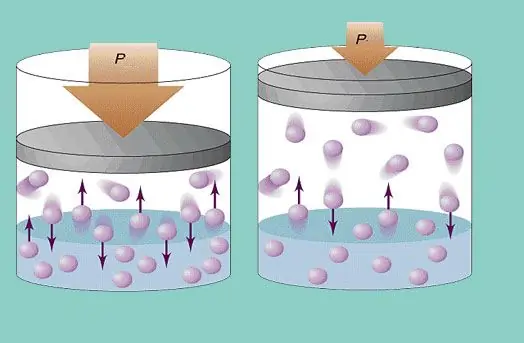
Model ideálního plynu předpokládá neustálý chaotický pohyb částic v systému a jejich neustálé kolize se stěnami nádoby. Každá taková srážka je považována za absolutně elastickou. Hmotnost částic je malá (≈10-27-10-25 kg). Proto při srážce nemůže vytvořit velký tlak. Nicméně počet částic, a tedy i počet srážek, je obrovský (≈1023). Kromě toho je střední kvadratická rychlost prvků při pokojové teplotě několik set metrů za sekundu. To vše vede k vytvoření znatelného tlaku na stěny nádoby. Lze jej vypočítat pomocí následujícího vzorce:
P=Nmvcp2 / (3V), kde vcp je střední kvadratická rychlost, m je hmotnost částice.
Absolutní teplota
Podle modelu ideálního plynu je teplota jednoznačně určena průměrnou kinetickou energií molekuly nebo atomu ve studovaném systému. Můžete napsat následující výraz, který souvisí s kinetickou energií a absolutní teplotou pro ideální plyn:
mvcp2 / 2=3 / 2kB T.
Zde kB je Boltzmannova konstanta. Z této rovnosti dostáváme:
T=m vcp2 / (3kB).
Univerzální stavová rovnice
Pokud zkombinujeme výše uvedené výrazy pro absolutní tlak P a absolutní teplotu T, můžeme napsat následující rovnost:
PV=nRT.
Zde n je množství látky v molech, R je plynová konstanta zavedená D. I. Mendělejevem. Tento výraz je nejdůležitější rovnicí v teorii ideálních plynů, protože kombinuje tři termodynamické parametry (V, P, T) a nezávisí na chemických vlastnostech plynového systému.

Univerzální rovnici poprvé experimentálně odvodil francouzský fyzik Emile Clapeyron v 19. století a poté ji do moderní podoby přinesl ruský chemik Mendělejev, a proto v současnosti nese jména těchto vědců.






