Jak víte, jakákoli fyzikální veličina patří do jednoho ze dvou typů, je buď skalární, nebo vektorová. V tomto článku se budeme zabývat kinematickými charakteristikami, jako je rychlost a zrychlení, a také ukážeme, kam směřují vektory zrychlení a rychlosti.
Co je rychlost a zrychlení?
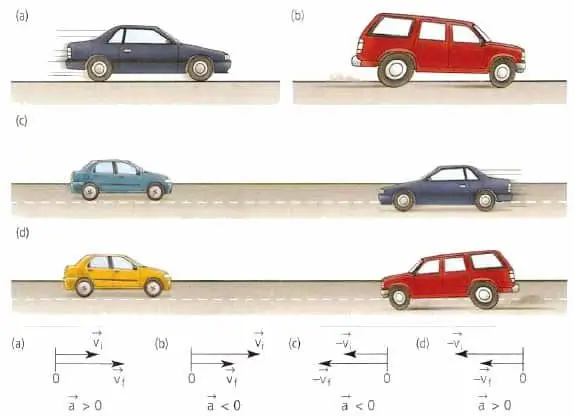
Obě veličiny uvedené v tomto odstavci jsou důležitými charakteristikami jakéhokoli druhu pohybu, ať už se jedná o pohyb tělesa v přímce nebo po zakřivené dráze.
Rychlost je rychlost, kterou se souřadnice mění v průběhu času. Matematicky je tato hodnota rovna časové derivaci ujeté vzdálenosti, tedy:
v¯=dl¯/dt.
Vektor l¯ je zde směrován z počátečního bodu cesty do koncového bodu.
Zrychlení je zase rychlost, se kterou se rychlost sama mění v čase. Ve formě vzorce to lze napsat takto:
a¯=dv¯/dt.
Samozřejmě, když vezmeme druhou derivaci zvektor posunutí l¯ v čase, dostaneme také hodnotu zrychlení.
Jelikož se rychlost měří v metrech za sekundu, zrychlení se podle písemného vyjádření měří v metrech za sekundu na druhou.

Kde jsou vektory zrychlení a rychlosti?
Ve fyzice je jakýkoli mechanický pohyb tělesa obvykle charakterizován určitou trajektorií. To druhé je nějaká pomyslná křivka, po které se těleso pohybuje v prostoru. Například přímka nebo kruh jsou hlavními příklady běžných cest pohybu.
Vektor rychlosti tělesa je vždy směrován ve směru pohybu, bez ohledu na to, zda těleso zpomaluje nebo zrychluje, zda se pohybuje po přímce nebo po zatáčce. Řečeno v geometrických termínech, vektor rychlosti je nasměrován tečně k bodu trajektorie, ve které se těleso aktuálně nachází.
Vektor zrychlení materiálu nebo bodu tělesa nemá nic společného s rychlostí. Tento vektor je směrován ve směru změny rychlosti. Například pro přímočarý pohyb se hodnota a¯ může buď shodovat ve směru s v¯, nebo být opačná k v¯.
Síla působící na tělo a zrychlení
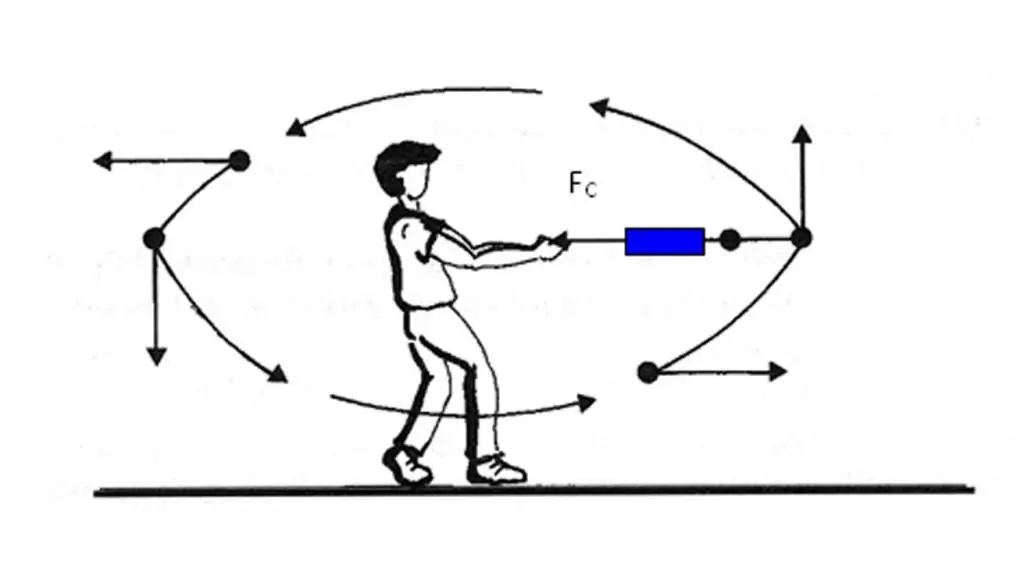
Zjistili jsme, že vektor zrychlení tělesa směřuje ke změně vektoru rychlosti. Není však vždy snadné určit, jak se rychlost mění v daném bodě trajektorie. Kromě toho je pro určení změny rychlosti nutné provést operacivektorové rozdíly. Abyste se vyhnuli těmto potížím při určování směru vektoru a¯, existuje jiný způsob, jak to rychle zjistit.
Níže je Newtonův slavný a všem studentům dobře známý zákon:
F¯=ma¯.
Vzorec ukazuje, že příčinou zrychlení těles je síla, která na ně působí. Protože hmotnost m je skalár, vektor síly F¯ a vektor zrychlení a¯ jsou ve stejném směru. Tuto skutečnost je třeba mít na paměti a aplikovat ji v praxi vždy, když je potřeba určit směr veličiny a¯.
Pokud na těleso působí několik různých sil, bude směr vektoru zrychlení roven výslednému vektoru všech sil.
Kruhový pohyb a zrychlení
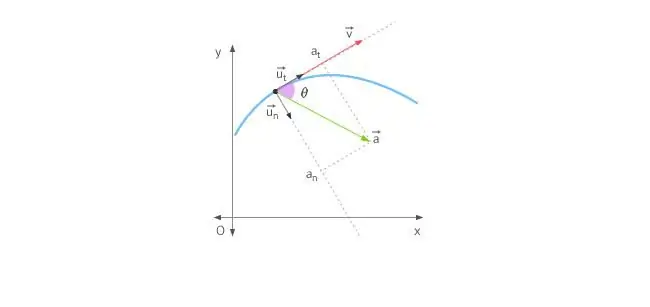
Když se těleso pohybuje přímočaře, zrychlení směřuje buď dopředu, nebo dozadu. V případě pohybu po kružnici je situace komplikovaná tím, že vektor rychlosti neustále mění svůj směr. S ohledem na výše uvedené je celkové zrychlení určeno jeho dvěma složkami: tečným a normálním zrychlením.
Tangenciální zrychlení směřuje přesně stejně jako vektor rychlosti nebo proti němu. Jinými slovy, tato složka zrychlení směřuje podél tečny k trajektorii. Tangenciální zrychlení popisuje změnu modulu samotné rychlosti.
Normální zrychlení směřuje podél normály k danému bodu trajektorie, přičemž se bere v úvahu její zakřivení. V případě kruhového pohybu udává vektor této složkydo středu, to znamená, že normální zrychlení směřuje podél poloměru otáčení. Tato složka se často nazývá dostředivá.
Plné zrychlení je součet těchto složek, takže jeho vektor může být nasměrován libovolně s ohledem na kružnici.
Pokud se těleso otáčí beze změny lineární rychlosti, pak existuje pouze nenulová normální složka, takže vektor plného zrychlení směřuje ke středu kruhu. Všimněte si, že toto centrum je také ovlivněno silou, která udržuje tělo na jeho trajektorii. Například gravitační síla Slunce udržuje naši Zemi a další planety na jejich oběžné dráze.






