V termodynamice je při studiu přechodů z počátečního do konečného stavu systému důležité znát tepelný efekt procesu. S tímto efektem úzce souvisí pojem tepelné kapacity. V tomto článku se budeme zabývat otázkou, co se rozumí izochorickou tepelnou kapacitou plynu.
Ideální plyn
Ideální plyn je plyn, jehož částice jsou považovány za hmotné body, to znamená, že nemají rozměry, ale mají hmotnost a veškerá vnitřní energie se skládá pouze z kinetické energie pohybu molekul a atomy.
Žádný skutečný plyn v ideálním případě nikdy nebude splňovat popsaný model, protože jeho částice mají stále nějaké lineární rozměry a interagují spolu pomocí slabých van der Waalsových vazeb nebo chemických vazeb jiného typu. Při nízkých tlacích a vysokých teplotách jsou však vzdálenosti mezi molekulami velké a jejich kinetická energie desítkykrát převyšuje potenciální energii. To vše umožňuje aplikovat s vysokou mírou přesnosti ideální model pro skutečné plyny.
Vnitřní energie plynu
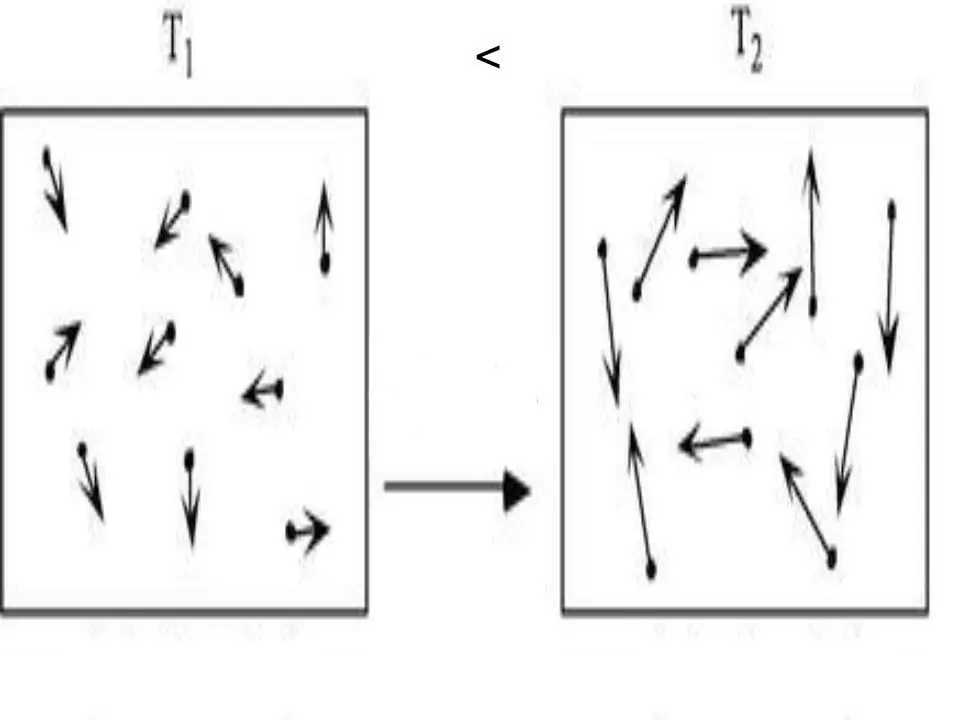
Vnitřní energie jakéhokoli systému je fyzikální charakteristika, která se rovná součtu potenciální a kinetické energie. Protože potenciální energii lze v ideálních plynech zanedbat, můžeme pro ně napsat rovnost:
U=Ek.
Kde Ek je energie kinetického systému. Pomocí molekulární kinetické teorie a aplikace univerzální Clapeyron-Mendělejevovy stavové rovnice není obtížné získat výraz pro U. Je napsáno níže:
U=z/2nRT.
Zde T, R a n jsou absolutní teplota, plynová konstanta a množství látky. Z-hodnota je celé číslo udávající počet stupňů volnosti, které má molekula plynu.
Izobarická a izochorická tepelná kapacita
Ve fyzice je tepelná kapacita množství tepla, které musí být poskytnuto studovanému systému, aby se ohřál o jeden kelvin. Platí i obrácená definice, to znamená, že tepelná kapacita je množství tepla, které systém uvolní, když se ochladí o jeden kelvin.
Nejjednodušším způsobem systému je určit izochorickou tepelnou kapacitu. Rozumí se jí tepelná kapacita při konstantním objemu. Protože systém za takových podmínek nevykonává práci, veškerá energie se vynakládá na zvyšování vnitřních energetických zásob. Označme izochorickou tepelnou kapacitu symbolem CV, pak můžeme psát:
dU=CVdT.
To znamená změna vnitřní energiesystému je přímo úměrná změně jeho teploty. Porovnáme-li tento výraz s rovností napsanou v předchozím odstavci, dospějeme ke vzorci pro CV v ideálním plynu:
СV=z/2nR.
Tato hodnota je v praxi nepohodlná, protože závisí na množství látky v systému. Proto byl zaveden pojem měrná izochorická tepelná kapacita, tedy hodnota, která se počítá buď na 1 mol plynu, nebo na 1 kg. Označme první hodnotu symbolem CV, druhou - symbolem CV m. Pro ně můžete napsat následující vzorce:
CV=z/2R;
CVm=z/2R/M.
Zde M je molární hmotnost.
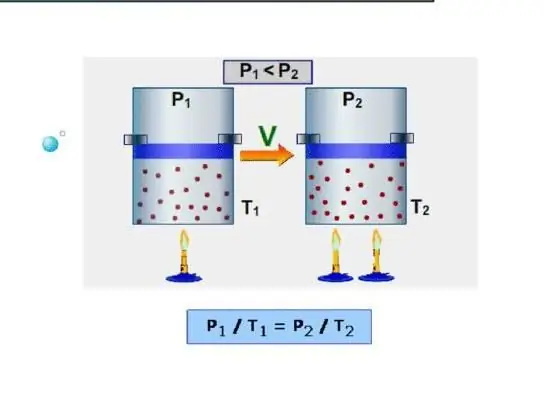
Izobarická je tepelná kapacita při udržování konstantního tlaku v systému. Příkladem takového procesu je expanze plynu ve válci pod pístem při jeho zahřívání. Na rozdíl od izochorického procesu se během izobarického procesu teplo dodávané do systému spotřebuje na zvýšení vnitřní energie a na provedení mechanické práce, to znamená:
H=dU + PdV.
Entalpie izobarického procesu je součin izobarické tepelné kapacity a změny teploty v systému, tedy:
H=CPdT.
Pokud uvažujeme expanzi při konstantním tlaku 1 molu plynu, pak první termodynamický zákon bude napsán jako:
CPdT=CV dT + RdT.
Poslední člen se získá z rovniceClapeyron-Mendělejev. Z této rovnosti vyplývá vztah mezi izobarickými a izochorickými tepelnými kapacitami:
CP=CV + R.
Pro ideální plyn je specifická molární tepelná kapacita při konstantním tlaku vždy větší než odpovídající izochorická charakteristika o R=8, 314 J/(molK).
Stupně volnosti molekul a tepelné kapacity
Napišme znovu vzorec pro specifickou molární izochorickou tepelnou kapacitu:
CV=z/2R.
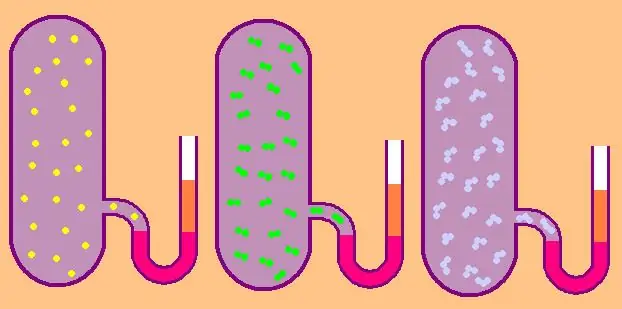
V případě monatomického plynu je hodnota z=3, protože atomy v prostoru se mohou pohybovat pouze ve třech nezávislých směrech.
Pokud mluvíme o plynu sestávajícím z dvouatomových molekul, například kyslíku O2 nebo vodíku H2, pak, kromě translačního pohybu se tyto molekuly mohou stále otáčet kolem dvou vzájemně kolmých os, to znamená, že z se bude rovnat 5.
U složitějších molekul použijte z=6. k určení CV






