Znalost definic ve fyzice je klíčovým faktorem pro úspěšné řešení různých fyzikálních problémů. V článku se zamyslíme nad tím, co se rozumí izobarickými, izochorickými, izotermickými a adiabatickými procesy pro ideální plynový systém.
Ideální plyn a jeho rovnice
Než přistoupíme k popisu izobarických, izochorických a izotermických procesů, uvažme, co je ideální plyn. Pod touto definicí ve fyzice uvažují systém sestávající z obrovského množství bezrozměrných a neinteragujících částic, které se pohybují vysokou rychlostí ve všech směrech. Ve skutečnosti mluvíme o plynném agregovaném stavu hmoty, ve kterém vzdálenosti mezi atomy a molekulami daleko přesahují jejich velikosti a ve kterém je potenciální energie interakce částic zanedbávána kvůli její malé velikosti ve srovnání s kinetickou energií.
Stav ideálního plynu je souhrn jeho termodynamických parametrů. Mezi hlavní patří teplota, objem a tlak. Označme je písmeny T, V a P. Ve 30. letech XIX stoletíClapeyron (francouzský vědec) nejprve sepsal rovnici, která kombinuje uvedené termodynamické parametry v rámci jediné rovnosti. Vypadá to takto:
PV=nRT,
kde n a R jsou množství látek a konstanta plynu.
Co jsou izoprocesy v plynech?
Jak si mnozí všimli, izobarické, izochorické a izotermické procesy používají ve svých názvech stejnou předponu „iso“. Znamená to rovnost jednoho termodynamického parametru během průchodu celým procesem, zatímco zbývající parametry se mění. Například izotermický proces ukazuje, že v důsledku toho je absolutní teplota systému udržována konstantní, zatímco izochorický proces ukazuje konstantní objem.
Isoprocesy je vhodné studovat, protože stanovení jednoho z termodynamických parametrů vede ke zjednodušení obecné rovnice stavu plynu. Je důležité poznamenat, že zákony plynu pro všechny tyto izoprocesy byly objeveny experimentálně. Jejich analýza umožnila Clapeyronovi získat redukovanou univerzální rovnici.
Izobarické, izochorické a izotermické procesy
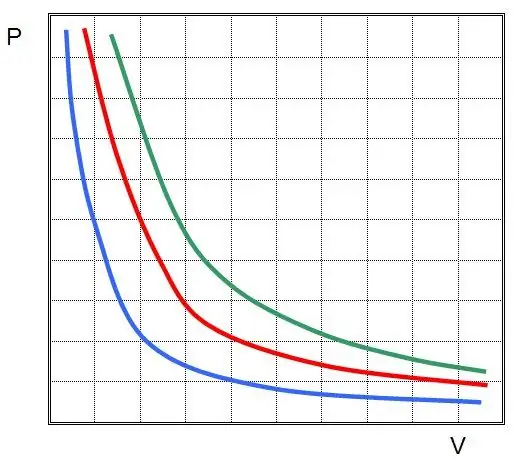
První zákon byl objeven pro izotermický proces v ideálním plynu. Nyní se tomu říká Boyle-Mariottův zákon. Protože se T nemění, stavová rovnice implikuje rovnost:
PV=konst.
Jinými slovy, jakákoli změna tlaku v systému vede k nepřímo úměrné změně jeho objemu, pokud je teplota plynu udržována konstantní. Graf funkce P(V) jenadsázka.
Izobarický proces - jedná se o změnu stavu systému, ve kterém tlak zůstává konstantní. Po zafixování hodnoty P v Clapeyronově rovnici získáme následující zákon:
V/T=konst.
Tato rovnost nese jméno francouzského fyzika Jacquese Charlese, který ji obdržel na konci 18. století. Izobar (grafické znázornění funkce V(T)) vypadá jako přímka. Čím větší tlak v systému, tím rychleji tato linie stoupá.
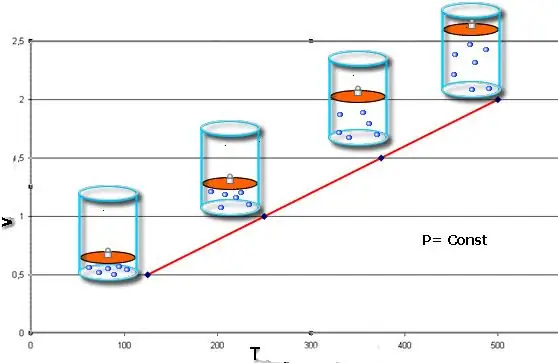
Izobarický proces lze snadno implementovat, pokud se plyn zahřívá pod pístem. Molekuly posledně jmenovaných zvyšují svou rychlost (kinetickou energii), vytvářejí vyšší tlak na píst, což vede k expanzi plynu a udržování konstantní hodnoty P.
Konečně, třetí izoproces je izochorický. Běží s konstantní hlasitostí. Ze stavové rovnice získáme odpovídající rovnost:
P/T=konst.
Mezi fyziky je známý jako Gay-Lussacův zákon. Přímá úměrnost mezi tlakem a absolutní teplotou ukazuje, že graf izochorického procesu, stejně jako graf izobarického, je přímka s kladným sklonem.
Je důležité pochopit, že všechny izoprocesy probíhají v uzavřených systémech, to znamená, že hodnota n je během jejich průběhu zachována.
Adiabatický proces
Tento proces nepatří do kategorie "iso", protože všechny tři termodynamické parametry se během jeho průchodu mění. adiabatickénazývá se přechod mezi dvěma stavy soustavy, ve kterých si nevyměňuje teplo s okolím. Expanze systému se tedy provádí díky jeho vnitřním energetickým rezervám, což vede k výraznému poklesu tlaku a absolutní teploty v něm.
Adiabatický proces pro ideální plyn je popsán Poissonovými rovnicemi. Jeden z nich je zobrazen níže:
PVγ=const,
kde γ je poměr tepelných kapacit při konstantním tlaku a při konstantním objemu.
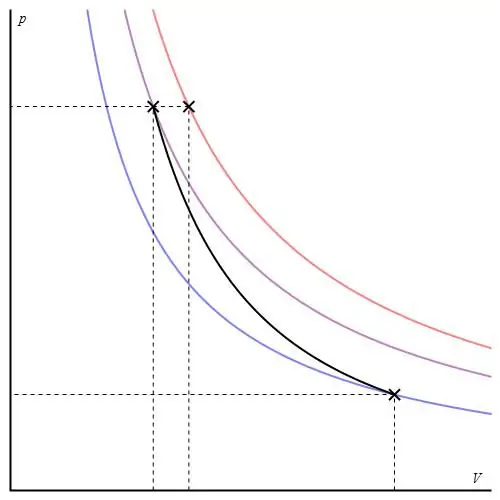
Adiabatický graf se liší od izochorického grafu procesu a od izobarického grafu, ale je podobný hyperbole (izotermě). Adiabat v osách P-V se chová ostřeji než izoterma.






