Plyny jsou z hlediska termodynamiky popsány souborem makroskopických charakteristik, z nichž hlavními jsou teplota, tlak a objem. Stálost jednoho z těchto parametrů a změna v ostatních dvou naznačuje, že v plynu probíhá ten či onen izoproces. Tento článek budeme věnovat podrobné odpovědi na otázky, že se jedná o izochorický proces, jak se liší od izotermických a izobarických změn ve stavech plynové soustavy.
Ideální plyn ve fyzice

Než odpovíte na otázku, že se jedná o izochorický proces, měli byste se lépe seznámit s pojmem ideální plyn. Ve fyzice se jím rozumí jakýkoli plyn, ve kterém průměrná kinetická energie částic, z nichž se skládá, vysoce převyšuje potenciální energii jejich interakce a vzdálenosti mezi těmito částicemi jsou o několik řádů větší než jejich lineární rozměry. Za uvedených podmínek je při provádění možnévýpočty neberou v úvahu energii interakce mezi částicemi (je rovna nule) a lze také předpokládat, že částice jsou hmotné body o určité hmotnosti m.
Jediný proces, který probíhá v ideálním plynu, je srážka částic se stěnami nádoby obsahující látku. Tyto srážky se v praxi projevují jako existence určitého tlaku v plynu P.
Zpravidla každou plynnou látku, která se skládá z relativně chemicky inertních molekul a která má nízký tlak a vysoké teploty, lze považovat za ideální plyn s dostatečnou přesností pro praktické výpočty.
Rovnice popisující ideální plyn
Samozřejmě mluvíme o univerzálním zákonu Clapeyron-Mendělejeva, kterému je třeba dobře porozumět, abychom pochopili, že jde o izochorický proces. Univerzální stavová rovnice má tedy následující tvar:
PV=nRT.
To znamená, že součin tlaku P a objemu plynu V se rovná součinu absolutní teploty T a množství látky v molech n, kde R je faktor úměrnosti. Vlastní rovnici poprvé sepsal Emile Clapeyron v roce 1834 a v 70. letech 19. století v ní D. Mendělejev nahradil soubor konstantních hodnot jediné univerzální plynové konstanty R (8,314 J/(molK)).
V souladu s Clapeyron-Mendelejevovou rovnicí zůstává v uzavřeném systému počet částic plynu konstantní, takže existují pouze tři makroskopické parametry, které se mohou měnit (T, Pa V). Poslední skutečnost je základem pochopení různých izoprocesů, které budou probrány níže.
Co je to izochorický proces?
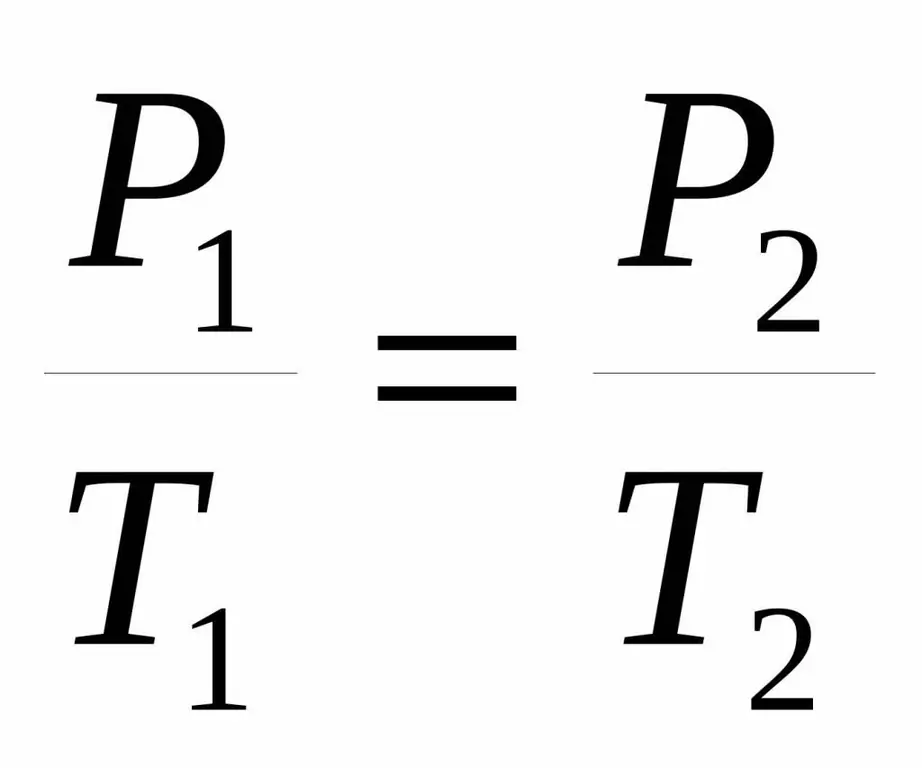
Tento proces je chápán jako absolutně jakákoli změna stavu systému, při které je zachován jeho objem.
Pokud se obrátíme na univerzální stavovou rovnici, můžeme říci, že v izochorickém procesu se v plynu mění pouze tlak a absolutní teplota. Abychom přesně pochopili, jak se termodynamické parametry mění, napíšeme odpovídající matematický výraz:
P / T=konst.
Někdy je tato rovnost uvedena v trochu jiné podobě:
P1 / T1=P2 / T 2.
Obě rovnosti se nazývají Karlův zákon podle jména francouzského vědce, který na konci 18. století experimentálně získal zmíněnou závislost.

Pokud sestrojíme graf funkce P(T), dostaneme přímou závislost, která se nazývá izochóra. Jakákoli izochora (pro všechny hodnoty n a V) je přímka.
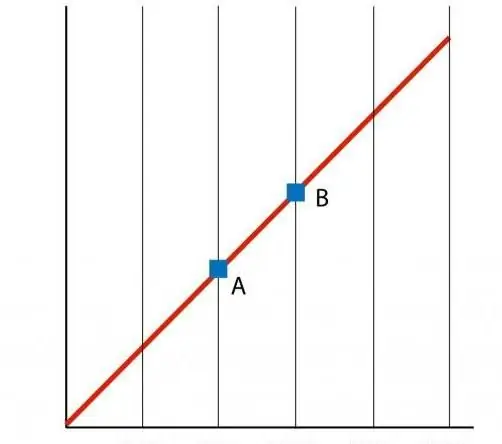
Energetický popis procesu
Jak bylo uvedeno, izochorický proces je změna stavu systému, která probíhá v uzavřeném, ale ne izolovaném systému. Hovoříme o možnosti výměny tepla mezi plynem a okolím. Obecně platí, že jakákoli dodávka tepla Q do systému vede ke dvěma výsledkům:
- mění vnitřní energii U;
- plynfunguje A, expanduje nebo stahuje.
Poslední odvození je zapsáno matematicky takto:
Q=U + A.
Izochorický proces ideálního plynu podle své definice neznamená práci vykonanou plynem, protože jeho objem zůstává nezměněn. To znamená, že veškeré teplo dodané do systému jde ke zvýšení jeho vnitřní energie:
Q=U.
Pokud do tohoto výrazu dosadíme explicitní vzorec pro vnitřní energii, pak teplo izochorického procesu může být reprezentováno jako:
Q=z / 2nRT.
Zde z je počet stupňů volnosti, který je určen polyatomickou povahou molekul, které tvoří plyn. Pro monatomický plyn je z=3, pro dvouatomový plyn - 5 a pro tříatomový a více - 6. Zde pod stupni volnosti máme na mysli translační a rotační stupně.
Pokud porovnáme účinnost ohřevu plynového systému v izochorických a izobarických procesech, pak v prvním případě dostaneme maximální účinnost, protože během izobarické změny stavu systému se plyn rozpíná a část tepelného příkonu je vynaložena na práci.
Izobarický proces
Výše jsme podrobně popsali, že se jedná o izochorický proces. Nyní si řekněme pár slov o dalších izoprocesech. Začněme izobarikou. Na základě názvu je chápán jako přechod systému mezi stavy při konstantním tlaku. Tento proces je popsán zákonem Gay-Lussac takto:
V / T=konst.
Stejně jako u izochory i izobara V(T) představuje v grafu rovnou čáru.
Prou jakéhokoli izobarického procesu je vhodné vypočítat práci vykonanou plynem, protože se rovná součinu konstantního tlaku a změny objemu.
Izotermický proces
Toto je proces, při kterém teplota systému zůstává konstantní. Je popsán Boyle-Mariottovým zákonem pro ideální plyn. Je zvláštní poznamenat, že se jedná o první experimentálně objevený zákon o plynu (druhá polovina 17. století). Jeho matematický zápis vypadá takto:
PV=konst.
Izochorické a izotermické procesy se liší z hlediska jejich grafického znázornění, protože funkce P(V) je hyperbolický, nikoli lineární vztah.
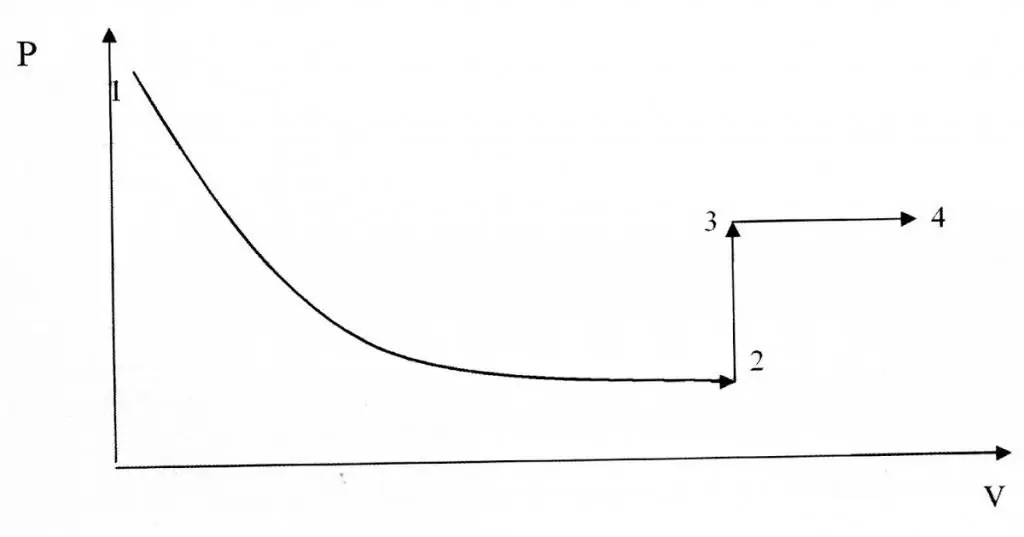
Příklad řešení problému
Pojďme konsolidovat teoretické informace uvedené v článku jejich aplikací k řešení praktického problému. Je známo, že čistý plynný dusík byl ve válci o tlaku 1 atmosféry a teplotě 25 °C. Po zahřátí plynové láhve a změření tlaku v ní se ukázalo, že je 1,5 atmosféry. Jaká je teplota plynu v láhvi po zahřátí? O kolik se změnila vnitřní energie plynu, pokud v balónu byly 4 moly dusíku.
K zodpovězení první otázky použijeme následující výraz:
P1 / T1=P2 / T 2.
Odkud získáváme:
T2=P2 / P1 T 1.
V tomto výrazu může být tlak nahrazen v libovolných jednotkáchměření, protože se zmenšují a teplota je pouze v kelvinech. Když to bylo řečeno, dostáváme:
T2=1,5 /1298,15=447,224 K.
Vypočítaná teplota ve stupních Celsia je 174 °C.
Vzhledem k tomu, že molekula dusíku je dvouatomová, lze změnu její vnitřní energie během zahřívání určit následovně:
ΔU=5 / 2nRΔT.
Dosazením známých hodnot do tohoto výrazu získáme odpověď na druhou otázku problému: ΔU=+12,4 kJ.






